轨迹命题(proposition of locus)是几何学研究的重要课题之一,叙述有关轨迹内容的几何命题,称为轨迹命题。轨迹命题有三种类型:1.在轨迹命题的结论中指明了轨迹的形状、位置和大小;2.在轨迹命题的结论中指明了轨迹的形状,但未指出其位置和大小;3.在轨迹命题的结论中未指明轨迹的形状、位置和大小。第一、二两种类型的轨迹命题具有定理的形式,所以称为轨迹定理;第三种类型的轨迹命题属于问题的形式,所以称为轨迹问题。例如,“和已知线段两个端点的距离相等的点的轨迹,是这条线段的垂直平分线”是第一种类型的轨迹命题;“和已知线段两端点距离相等的点的轨迹是一条直线”是第二种类型的轨迹命题;“求和已知线段两个端点的距离相等的点的轨迹”是第三种类型的轨迹命题。对于第一种类型轨迹命题,只需对命题加以证明;对于第二种类型轨迹命题,需在明确轨迹位置和大小之后,对命题加以证明。对于第三种类型轨迹命题,要首先探求轨迹的形状、位置和大小,然后给以证明.对于后两种类型的一些轨迹命题,有时还要给以必要的讨论,以推究轨迹可能发生的变化1。
轨迹命题的基本性质符合某个条件的点的轨迹是图形F,也就是说:
(1 )若点A符合某个条件 点A在图形F上;
点A在图形F上;
(2)若点A'在图形F上 点A'符合某个条件。
点A'符合某个条件。
用以上两个命题的等价命题表述为:
(1')点B不在图形F上 点B不符合某个条件;
点B不符合某个条件;
(2')点B'不符合某个条件 点B'不在图形F上2。
点B'不在图形F上2。
(1)和(1')保证了没有一个符合条件的点不在图形F上,亦即符合条件的点一个也没有遗漏掉,这叫做轨迹的完备性,另一方面,由于它说明了任意一个点只要合乎某条件就能充分保证它在这个图形上,因而也叫做充分性。
(2)和(2')保证了图形F上的点没有掺杂一个不符合条件的点,这叫做轨迹的纯粹性。另一方面,由于它说明了点要在图形上,就非合乎某条件不可,因而也叫做必要性。
两方面合起来,保证了轨迹上的点不漏不杂。完备性和纯粹性是轨迹的基本属性。轨迹命题的证明必需完成以下两步: (1 )证完备性;( 2)证纯粹性2。
轨迹命题的证明为了确认轨迹命题的真实性,证明轨迹命题“合乎某条件的点的轨迹是图形F”,要包括两方面的证明:
1.完备性。任取符合某条件的一点P,证明P在图形F上。
2.纯粹性。在图形F上任取一点P′,证明P′符合某条件。
也可证明1和2的等价命题:
1′.不在图形F上的点Q不符合条件。
2′.不符合条件的点Q′不在图形F上。
综上所述,证明完备性时,可证1或1′,证明纯粹性时,可证2或2′,因此,对一个轨迹命题的证明有四种证法:证1和2,证1和2′,证1′和2,证1′和2′,究竟选用哪种证法要根据实际情况,以便于思考和证明简捷为选用标准.真实性得到证明的轨迹命题,称为轨迹定理。
因为初学者对逆否命题不大熟悉,所以—·般多应用第一种,即证明1,2成立,如果第一种不好考虑,再考虑第二、三种,最后考虑第四种。
在初等平面几何中,通常考虑的轨迹是:线段,直线,圆、圆弧等;在立体几何中则要考虑平面,球面,旋转曲面等;在解析几何中,点的轨迹表现为点的坐标满足一个或几个方程或不等式,而满足方程或不等式这个事实恰恰是集合的点所具有的特殊性质。它将主要研究圆锥曲线及超越曲线。
轨迹命题的三种类型轨迹命题一般按其结论分为三种类型:
①如果给出了轨迹的条件,在结论中又指出了轨迹的形状、位置和大小(如果有大小的话),如“和两条平行的定直线等距离的点的轨迹是平行于定直线,且距两定直线等远的一条直线”这类轨迹命题叫做第一种类型轨迹命题;
②如果给出了轨迹的条件,在结论中又指出了轨迹的形状,但没有指明轨迹的位置和大小(如果有大小的话),如“和两条平行的定直线等距离的点的轨迹是一条直线”这类轨迹命题叫做第二种类型轨迹命题;
③如果只给出了轨迹的条件,没有指出轨迹的形状、位置和大小(如果有大小的话),如“求和两条平行的定直线等距离的点的轨迹”这类轨迹命题叫做第三种类型轨迹命题。
第一种类型轨迹命题,有条件,又有完全的结论,故可称为轨迹定理.第二种类型轨迹命题,有条件,有不完全的结论,也可称为轨迹定理.第三种类型轨迹命题,只有条件,没有结论,属于问题的形式,因此称为轨迹问题3。
基本轨迹命题基本轨迹命题1和一个已知点的距离等于已知长的点的轨迹,是以已知点为圆心,已知长为半径的圆.如图1,⊙O是和定点O的距离等于定长r的点的轨迹。
基本轨迹命题2和两个已知点距离相等的点的轨迹,是连结这两点的线段的垂直平分线。如图2,直线l是和已知点A,B距离相等的点的轨迹。
基本轨迹命题3在一个已知角内和角的两边距离相等的点的轨迹,是这个角的平分线。如图3,射线OC是∠AOB内和两边OA,OB距离相等的点的轨迹。
推论和两条相交的已知直线距离相等的点的轨迹,是这两条直线所成两组对顶角的平分线。如图4,l1,l2是和两相交直线AB,CD距离相等的点的轨迹。
|| ||
基本轨迹命题4和两条平行线距离相等的点的轨迹,是和这两条平行线距离相等的一条平行线。如图5,直线l是和两平行线AB,CD距离相等的点的轨迹。
基本轨迹命题5和已知直线的距离等于定长的点的轨迹,是平行于这条直线并且和这条直线的距离等于定长的两条直线。如图6,直线l1,l2是和直线AB距离等于定长k的点的轨迹。
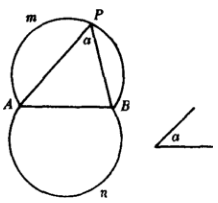
基本轨迹命题6和已知线段的两个端点的连线的夹角等于已知角的点的轨迹,是以已知线段为弦,所含圆周角等于已知角的两段弧(端点除外)。如图7,弧和是和线段AB的两个端点的连线的夹角等于已知角a的点的轨迹3。
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所



 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国
