科普中国-角平分线定理

从一个角的顶点，在角内引出一条射线，把这个角分成两个大小相同的角，则这条射线叫作这个角的角平分线。角平分线定理描述了角平分线的若干性质，包括：角平分线上的任意一点到角两边的距离相等；三角形角平分线分对边比例与另两边比例相等。

角平分线定理在多个领域都有着重要的应用，如建筑设计、航海航空、光学系统分析等。

定理内容

定理一

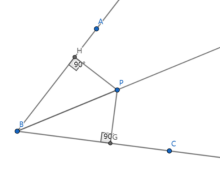
角平分线上的任意一点到角两边的距离相等。

如图，是平分线上一点，过点作于，作于，则：

定理二

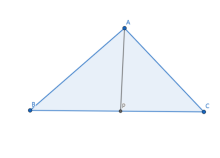
三角形角平分线分对边比例与另两边比例相等。

如图，是上一点，是的角平分线，则

定理一的逆定理

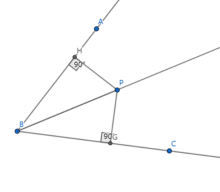
角内到角两边距离相等的点在该角的角平分线上。

如图，若过点作于，作于，有，那么在平分线上，即平分。

定理二的逆定理

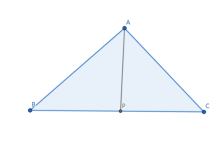
三角形边上某一点分该边比例与另外两边比例相等，则该点与对角顶点的连线是对角的角平分线。如图，若边上一点满足

则是的平分线。

定理证明

定理一

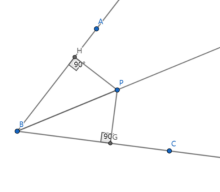
证明：

由于是的角平分线，故。

又由于，，故

于是，在和中

从而（全等三角形判据：AAS），故，得证。

定理二

正弦定理证明

证明：

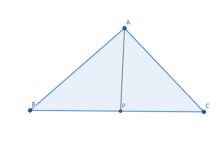
在中由正弦定理得：

在中正弦定理得：

由于，，故：，。由此得到

即

得证。

构造平行线证明

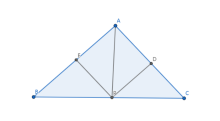
证明：

如图，过点作的平行线交于，作的平行线交于。

于是，，是两两相似的，可得

由平行线还可得四边形