新的时代，我们需要什么样的学习能力？

培根有名言：知识就是力量。但是，只有理解了的知识才是力量，只有善于思考的人才富于创造性。今天，科技的进步和人工智能的发展，已经对人的智力提出了新的要求。旧时代人们尊崇那些拥有渊博知识的人，而在当代，只有能够深入理解和创造人类知识的人才是真正拥有杰出头脑的人。本文对于达成这样的目的提供了一种方法和思想，虽然看似研究的是“教”与“学”的问题，但其读者并非局限于学生和教师。应该说，它更适用于类似科学家、社会科学研究者和领导者，或者像这类人一样思考问题的人。

祝《返朴》的读者在新的一年都能拥有更棒的头脑，和健康的体魄！

撰文 | 吴金闪（北京师范大学系统科学学院教授）

大家都知道学习是需要方法的，可是具体这个方法是什么，就不知道了。一个偷懒的或者无奈的回答是：无一定之规。我们看到很多学习很好的学生并不是把时间基本上都花在学习上。我自己当学生的时候就是这样的一个人。可是，当我们思考，或者被问，到底什么学习方法使我们达到了这个效果的时候，我们通常说不出一个所以然来。我记得我自己曾经给出的答案是多想，随便想，不限制地想。尽管现在我已经知道这个答案其实有道理（这个道理在本文中会用概念地图理解型学习来解释），但是，听者和问者能从这个答案里面悟出多少就很难说了。我们还有这样的一些经验或者体会：有些人当她们对一个领域熟悉到一定程度之后，她们可以“灵机一动地”或者“深思熟虑地”建立这个领域与其他领域的联系；还有的人，他们可以提出和解决非常深刻非常困难的问题，而且往往这样的解决问题的方法可以成为解决其他问题而不仅仅是原来的问题的基础。我们往往把这样的人称作创造力很强的人。如果我们问这样的人，什么提升了其创造性，能够说出一个道理来的也不多。我自己也应该算这样的人，常常会把不同领域的东西联系在一起，也常常思考一门学科里面最深刻的几个问题中的一两个，尽管已经解答的还不是很多。如果问我，事实上我也确实被问过，我的答案也基本上是多想，随便想，不限制地想。可以算是略有小成的物理学家汤超——沙堆模型的原创者之一[1]——也被问过这个问题。他经过几分钟的思考之后，以开玩笑的方式，给出的答案是，多看、多想、多聊。尽管现在我知道这个答案很有道理，但是听者和问者能够从这个答案中悟出真知的人也是少数。所以，高效率的学习和思考都是需要而且有方法的。这个道理大家都明白都同意。可是，方法是什么不知道。

高效率的教学也是需要而且有方法的。教学就是为了让学生学会学习和思考，既然学习和思考是需要而且有方法的，那么教学自然也是需要而且有方法的。可是这个问题比前者还要难，可供参考的方法还要少。我们大概都听说过，“教学是一门艺术”。凡是艺术就意味着能够一般化程序化的东西少，个性化的东西多。很多有名的教师，例如Richard Feynman ——费曼物理学讲义的作者、天才物理学家，Leonard Susskind——超弦理论的创立者之一、一系列斯坦福大学理论物理公开课的主讲人，Michael Sandel——哈佛大学“Justice（正义）”公开课的主讲人，Ben Polak——耶鲁大学“Game Theory（博弈论）”公开课的主讲人，都不是学教育出身，而是从自身的研究工作和研究领域出发体会出来的。好吧，既然如此，我们有没有一些方法能够提高教学的效率呢？有，但是，一般性的方法很少很少，不过，我们即将介绍的概念地图教学方法就是一个。

学科大图景

我们这里要介绍的概念地图理解型学习是从“低能近似”的层次的研究中——“低能近似”不太好听，我们给取它一个名字， 唯象研究，就是基本上从现象出发的，基本原理还不太清楚的研究——提出来的有效的学习和教学方法。除了这个提高学习和教学的效率的目标，更具体地，这个方法主要解决什么问题呢？解决学什么、怎么学，教什么、怎么教的问题。千万不要认为学什么、教什么的问题是一个平庸的问题。当然，如果你认为什么都应该学应该教，学生就是应该尽可能地多学点，那么你不是本文的读者。学生的总的时间是有限的，学习文化知识的时间更应该是有限的。学生的时间还需要花很大一部分来接触不同的事物，了解和欣赏自然界，交朋友，发呆，爬树，钓鱼，游戏，运动，跟家人共度家庭时间，等等等等。花在任何一本不值得的书，或者一门不值得上的课，一个不值得学的知识点上的时间就意味着减少了本来可以用来增加生活体验和生活乐趣的时间。尤其是当老师的我们，每一次我们没有选择最合适的内容来教的时候，我们都在强制学生跟我们一起浪费时间，而且是很多的学生，并且是不得不跟我们一起浪费。因此，仔细地审视每一项教学内容的必要性合理性是老师一定要去做的事情。当然，如果你是那种拿过一本书来就教，现在不主动思考教什么的问题，将来也不打算思考的老师，那么，你不是本文的读者。

那么，学什么、教什么？举个不太恰当的例子，而且正因为不恰当，反而更深刻。很多家长在孩子们很小的时候就教孩子们算加减法。很多孩子们对于加减法的认识是记忆性的，而不明白加减法的含义。也就是说，孩子们在开始的时候，不知道 1 + 1 = 2 意味着“一个单位的某种东西加上另外一个同样的单位的同样的东西，就是两个单位的同样的东西”这个含义，但是已经能够回答大人们问的问题，“某某， 1 + 1 等于几呀？”。某些家长还为此偷偷地高兴很多天。我现在要写下来的论断是：如果仅仅考虑加减法本身，除了为了明白加减法的含义需要一定量的计算练习，孩子们永远不应该学习加减法的计算。任何加减法，只要孩子们已经能够把实际问题转化成加减法的问题，那么学习的任务已经完成了。当然，为了熟练地在实际问题和数学表达式之间做转换，一定量的练习是必要的。但是，数学绝对不是做算术运算，这些运算的事完全可以交给计算器。同样地，所有的微积分也不要学生去熟练去记忆，只需要学会把实际问题转化成微积分的表达式。转化完成之后，我们有 SageMath[2], Maple[3]之类的专门的工具来完成它。所以，为了算术而学算术，为了微积分而学微积分，可以休矣。

那么，数学到底应该学什么教什么，算术和微积分的运算，需要熟练吗？需要，但是完全是因为其他原因。在数学上有一定造诣的读者会明白，因式分解是重要的思考方法，很多困难的问题可以用因式分解的思路变得更简单。要做好因式分解，需要对整数的加减乘除具有很好的感觉。熟悉算术运算就是为了培养这个感觉。变量替换和模块化在分析很多复杂的问题中非常重要，足够的微积分运算的训练可以得到一双敏锐的眼睛，提示你做合适的变量替换和把问题模块化。所以，这两个不太合适的例子很好，我很喜欢。也就是说，一个东西值不值得学，值不值得教，除了考虑学生和老师作为个体的兴趣（这个我们不管，有的人就是喜欢做一本百科全书，喜欢去挑战王小丫、李咏、汉字英雄、我爱记歌词，这是他们的自由。对了，这样的人也不是本文的读者。），最主要的是看学了这个东西可以用来理解或者创造性地运用哪些其他的东西或者解决什么样的问题，看这个东西在整个学科里面的地位，体现了这个学科的学科大图景的哪些方面。当然，我这里假设我们的教学的终极的目标，是培养一个个探索这个世界的人，不管是这个世界的人类行为的还是自然行为的方面。所以，我隐含了我所谈的培养的对象实际上是类似于科学家、社会科学研究者、领导者的人，或者象科学家、社会科学研究者、领导者一样思考问题的人。

回到我们的主题，在学科教学、学校教学的层面，学什么、教什么是个大问题。那么如何确定学什么、教什么呢？我们说要看一个内容在整个知识框架或者说学科大图景中的地位。那么，如何确定一个内容在整个知识框架或者说学科大图景中的地位呢？要依靠概念地图。如何运用概念地图来确定一个内容在整个知识框架或者说学科大图景中的地位呢？这个我们将来再展开讨论。在那之前，我们一定要看见，随着技术的进步，电子终端随处可见，搜索引擎越来越准确，人们对于记忆性的知识本身的需求越来越少，对于成为一个知识渊博的人的需求越来越小，同时创造性地运用和创造知识的需求越来越高。而理解知识是创造性地运用和创造知识的基础。我们学习和教学中的内容应该越来越少地关注能够通过简单提问谷歌（Google） [4]或者 Siri[5]就能解决的问题，更多地关注提出以前没有人提出过的问题，回答以前没有人回答过的问题，用新的方式回答问题，给一个问题提供新的答案，关注如何促进人类文明的进步。

那么，提出问题、解决问题、创造知识、创造性地运用知识、理解知识，靠什么？靠对一个或者多个学科的学科大图景的理解和把握。也就是，靠明白和体会到这个学科的研究者的典型思维方式和典型分析方法，靠了解这个学科的研究者大概研究什么典型对象、这些典型对象的什么典型问题，靠了解了典型思维方式、典型分析方法、典型对象、典型问题之后，体会到这个学科和世界的关系和其他学科的关系。于是，有一天当你面对相关的对象的相关的问题的时候，你知道把问题表述成相关学科的问题，用相关学科的思维方式和分析方法来尝试解决这个问题，甚至通过解决这个问题发展新的思维方式和分析方法。

例如，对于物理问题，我们一般问：状态如何描述、状态是否会发生变化呢，如果变化其变化的原因是什么；当我们来思考变化原因的时候，我们经常从事物的相互联系的角度来思考，看看这个对象受哪些东西的作用或者说影响；在真的来写下来状态描述和状态变化的原因的时候，我们经常用数学结构和数学方程；最后，一般来说，判断我们的数学结构和数学方程对错的标准是，考察一个类似的新现象，用这些数学结构和数学方程对这个现象算一算，看看算出来会发生什么，然后把这个“算出来的发生什么”和实际拿这个现象做一个实验和测量得到的“实际发生什么”做一个比较。用更加专业的名词来说，这几个分别叫做“力学世界观”、“相互作用”、“运动方程”、“数学建模”、“实验和测量”、“可验证性”。那学习物理学，除了学会具体的针对某些现象的方程和具体的方程的求解之外，还要体会好这几个名词——它们真正地代表了物理学是什么。这就是物理学的学科大图景：一般来说，我们关心这个世界的自然的那部分谜题，而我们关注的问题大多数是我们如何用数学模型和计算的方式来描述或者解开这个谜题，其中解开的标准不过就是我们算出来的和实验测量出来的结果在误差范围内相符，同时，大多数这样的数学模型我们都是从个体和个体之间的相互作用的角度采用分析和综合的视角来构建的。

搞清楚了这个学科大图景，当然还有其他在更具体的问题上的典型分析方法和典型思维方式，例如对称性在电磁场的数学模型中的作用、对称性对整个物理学理论的影响、关联函数和相变在物理学和物理学之外的方法论上的意义，等等，下一步的问题，就是找出来合适的具体问题和具体知识，当做例子，来展示学科大图景中的一项或者多项，促进学习者对学科大图景的理解。这是一个双向的过程：在学习每一个具体问题和具体知识的时候，尽量提炼出来能够帮助学生体会的学科大图景；针对每一个你已经提炼出来的学科大图景，找到最合适的具体问题和具体知识当例子。

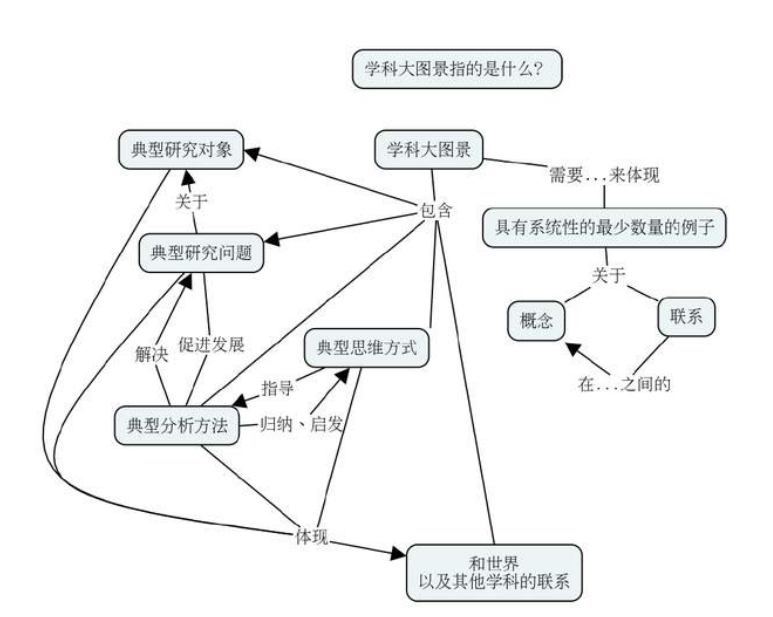
图：什么是一个学科的学科大图景：就是这个学科的研究者的典型研究对象、典型研究问题、典型思维方式、典型分析方法、和世界以及其他学科的关系。

除了具体知识、具体问题和学科大图景的联系，另一个重要的联系，是知识之间的联系。一般来说，一个比较成熟的学科，总是会找到一些基本概念和基本假设，然后，把其他的概念看做是这些基本概念和基本假设，通过一般性的人类逻辑或者这个学科的典型思维方式和分析方法（当然，它们也满足一般性的人类逻辑的约束，可以看作是会一般性的人类逻辑在这个学科里面的具体表现），来得到其他的知识。那么，在我们以学科大图景为目标而学习的过程中，也要整理和运用好这个概念之间的联系。通过这个概念之间的联系，我们也可能更好地找出来比整个学科的概念集合少的多很多的关键概念关键知识来构建整个学科的知识，来体验整个学科的大图景。这也就是概念地图理解型学习中的“系联性思考”的含义。在这里，需要强调，学科大图景以及帮助学习者体会好学科大图景的最少量的最关键的具有成长性——通过联系来成长——的具体知识和具体问题的例子，才是学什么和教什么的答案。另外， 概念地图理解型学习也是学什么和教什么的一部分。这样学到的学科大图景和具体知识、学习方法，也会同时让学习者感受到这个学科的魅力，从而形成对这个学科的情感。这些才是应该教和学的东西。

这样的学习，和很早的时代那种以渊博的知识为目标的学习是完全不一样的。那个时代能够有机会学习知识，能够有知识可以学习，能够将来有口诀和记住的表可以查，就已经是很了不起的少数人才能做的事情了。

再举一个例子来说明新时代的学习内容的变化。考虑你的一次出行。你的目标是从你熟悉的区域 Z，你需要到达一个你不太熟悉的地点 O。如果没有地图，你需要请教熟悉这两个地区，甚至中间可能需要经过的所有的地区的专家来制订一个出行路线。而且，这个出行路线在什么地方转弯都需要记下来，在心里或者在一张纸上。而且，我们不能保证经过咨询专家得来的路线是路程最短的还是开车或者走路最方便的。这个没有整体地图，只靠行路的人局部探索和专家指导的出行模式——这样的指导也基本上依赖于记忆型知识，就是古老的， GPS 定位技术普及之前的，最可靠的出行计划。现在有了地图和电子地图，我们再也不需要能够记住这些区域的纯粹知识型的专家了，我们需要的是及时更新的路况信息和好的路径搜索算法，一个处理地图以及交通信息的“专家”。当然，实际上，我们发现，除了专门研究这样的算法的人，一般人连这个算法都可以用手机上的计算核心以及所运行的程序来替代。也就是说，现在，你只需要一个地图，一个定位系统，一个路径搜索算法，然后你就出门吧。基本上我们就没有任何记忆的需求了。当然，现实的世界中，我们会遇到地图没更新、算法有 bug、算法可能比较慢等之类的问题，我们还不能完全不识路，少量的路标可能还是需要记忆的。

前两天发生在我自己和我的孩子身上的在商场寻找厕所的事情，可以给我们更深刻的学习方法方面的启发。我们需要在一个完全不熟悉的商场中找到厕所。首先，我们看了一下标志牌，没看明白指示。然后，我们问了问路，得知在某一个角落里面有，而且得到了如何“拐弯抹角”的具体路线。

但是，非常不好意思的是，路线对我来说比较复杂，没记住。不过，两件事情我记住了：这一层有厕所，而且在那个方向上。于是，我就和孩子一起出发去寻找厕所。经过好多个拐弯——后来发现多走了一些弯路——之后，就找到了厕所。在这个找厕所的事情里面，知道并且相信某个范围内有厕所， 而且知道大概的方向，就足够了，而不用记住具体明确的路线。找到厕所的当时，我就想起学习这件事情来：在学习的时候，明白并且相信某个东西——例如课程或者书——里面有值得你学习，你喜欢学习，或者能够解决你的问题，满足你的好奇心的东西，是最重要的。然后，学习的时候要做到有方向感——可以来自于自己的积累、直觉，也可以来自于老师或者同学的启发。就是这个信念和方向感，而不是具体的定义和计算——当然，在真的要理解所学内容的时候，深刻理解这些定义和计算是非常重要的[6]——就能基本上保证你学得懂学得到，尽管可能要走一些弯路。

上面的 GPS 的例子的启发是，随着时代的进步，我们对纯粹记忆型知识的需求会越来越低，而这个寻找厕所的例子则告诉我们，信念和方向感对于学习和研究工作来说比具体的知识更加重要。当然，你会问这样的信念和方向感从哪里来。如果有指导老师和学习小组，那么，这个信念和方向感可以来自于这样的先行者。但是，既然我们强调自学，那么在基本上靠自己学习的时候，这样的信念和方向感又从哪里来呢？来自于对自身的兴趣和能力的了解，以及来自于对已经学会的知识的全局性的大图景的把握。那么，如何从所学的具体知识中把握好大图景呢？我们下面就讨论怎么学、怎么教的问题。

创造体验式学习

现在，我们来把上面那个妈妈带着孩子展示 1 + 1 的例子补充完。从中体会到底应该如何学习。我从小就不懂事尽说真话。有一天有一个妈妈抱着她大约两岁的小孩，特别自豪地说我家孩子会算 1 + 1 了。然后，一群人就起哄，说演示一下呗。妈妈就问孩子“某某， 1 + 1 等于几啊”。孩子就答“2”。然后，妈妈就抱着孩子自豪地转了一个圈，准备走了。这时候，我不懂事地跳出来问，“某某，那你知道 1 是什么意思， 2 是什么意思， + 是什么意思， =是什么意思吗？”然后，孩子和妈妈被我搞得灰头土脸走了。我不是希望大家都像我这样不懂事，尽管，我到今天仍然尽说大实话。我只是强调，如果要理解 1 + 1 = 2 的含义——把一个在某个单位下数一数得到数量是 1 的东西和另一个在“同一个单位”下的数一数得到数量是 1 的东西“合起来数一数”得到数量是 2，那么我们是需要一些基础的——对数一数和数量的理解、对单位以及单位可变换和保证相同单位（例如一双袜子和一双袜子加起来是两双，但是一双袜子和一只袜子就不好办了）的理解，对“加法就是合起来数一数”的理解，对“等号表示数量相等，形式上一般不完全相同”这个含义的理解。在建立对这些东西的初步理解之前，尽管随着进一步学习将来可以深化，不应该直接学习加法计算。这样的在没有搞清楚上面的东西的理解之前的加法计算的学习，基本上只能成为记忆，依靠记忆和重复来学习，称为“机械式学习”。那么，是不是如果不考虑学习成本，其实，主要依靠记忆和重复的机械式学习其实也不错呢，也可以成为主要的怎么学怎么教的方法之一呢？不能。因为从机械式学习中，我们不能学会学科大图景。

再一次回到学什么、教什么。我们说了，学习的根本目的是为了提出问题解决问题，为了理解世界，为了让世界更美好。固然，大部分所要解决的问题都是曾经有人遇到过的问题，于是，你只需要有一个别人是怎么解决这个问题的数据库就可以，从里面查出来前人是怎么解决的，然后照搬或者稍微改造一下就可以用来解决你面对的问题。但是，科学的进步、社会的发展的根本是提出和解决新问题。当你面对一个别人从来就没有解决过的的问题的时候，更加重要的，就不再是答案的数据库，而是前人在解决相关问题的过程中提炼出来的典型思维方式、典型分析方法。甚至，前人提出问题的时候的经验和感悟，也可能可以帮助你来提出新的问题。而这些，通过重复、记住、查表的方式，都是不能完成的。这就是为什么我们要否定机械式学习。

当然，否定机械式学习并不意味着，学习者就不需要和不能运用记忆这个工具了。首先，有一些技巧性比较高的东西，只有通过一定量的练习之后，才能习得。例如演奏音乐的练习，除了懂得道理，甚至还需要形成肌肉记忆。

其次，有一部分知识，记忆和理解可以相互促进。记住一些东西有助于更快地反应过来，从而更方便建立联系，促进理解；同时，有些东西理解了之后，记起来就会效率更高。例如，在理解了一个字和这个字的组成部件之间的关系（比如说，可能一个部件表示含义，另一个部分表示读音）之后，可以更好地记住和运用这个汉字。最后，甚至有的时候通过理解和联系之后，自己总结出来一些口诀，来帮助更快速地解决问题，也不是不可以。例如，通过多次计算个位数的加法，你再也不用数手指头来计算加法了而实际上脑子里面形成了一章加法表。例如，通过多次计算个位数的乘法，你不用每次把乘法——重复多次的加法——变成加法来计算了，而是在脑子里面形成一张乘法表来计算了。这些都是记忆这种学习方法可以发挥作用的地方。我们所反对的是，直接把对知识的记忆，对口诀的记忆当做学习的目标和手段，来教和学。让学习者经历提出问题、解决问题、建立联系来理解这个问题和解决方法的过程甚至痛苦和快乐，然后，最好通过自己的整理和总结来形成记忆，这样的记忆型的学习可以有。

提起来这个机械式学习学习，我还想分享一个例子。受“海量阅读”、“名著阅读”思潮的影响，最近看到中考和高考语文题当中出现了“名著主要内容”形式的问题。例如，问《海底两万里》中有哪一些主要角色、他们之间主要发生了什么，问《三国演义》空城计中主要人物是谁、发生了什么事情，问某某书的主要写作特点是什么，等等。固然，这些题的本意是刺激孩子们去阅读名著。但是，只要题目是这样出的，那么，将来自然会出现“名著导读”、“名著代读”类型的学习参考书。这些书会把考试范围内的名著的主要内容和写作特点做一个精炼的总结，学生只需要把这些总结背下来，就可以在这样的考试中获得高分。于是，还是不可能推动学生真正自己去做名著阅读。机械式学习是短期提高成绩的捷径，是长期真正学习到学科大图景的障碍。那么，回到语文的学习，我们希望学生阅读名著到底为了什么？是不是提高阅读能力、写作能力，尤其是书面语和有关稍微抽象一点的主题的阅读和写作？如果是，那么，是不是可以不通过考“名著主要内容和写作特点”的考题来检验是否达成了学习效果？从而，也使得在语文的教和学中，也不依赖“名著导读”、“名著代读”、“精炼总结”等等纯粹重复和记忆式的学习？

回到我们的主题，那么，当我们否定了机械式学习，到底怎么学习呢？这里我们还是用出行计划的例子来讨论这个问题，不过，这里用它的抽象含义，类比含义，而不是真的出行。假设，你的学习目标就是你要到达的尚不熟悉的概念 O。现在，你需要从你熟悉的领域 Z 出发，学习到 O。怎么办？如果我们有一个地图，一个关于这些概念之间的关系的地图，我们就可以从 Z 开始，通过概念之间的联系来习得 O。同样地，如果我们面对一个证明题，要证明的目标是 O，起点是区域 Z 中的已知定理、公理和定义，那么我们需要构建的也是从 Z 到 O 的道路。这个时候，有一个包含了 Z 和O 以及大部分中间概念的知识的地图就会发挥非常大的作用，大大提高我们学习和思考的效率。正像实际的地图在我们制订出行计划的时候的重要性，对于理解概念、运用知识和创造知识来说，概念地图就是我们认知结构中的地图。所以，怎么教怎么学，还是依赖于这个地图。这个时候，如果我们在已有的两个概念之间新建立了一个的联系，实际上就是相当于新建设了一条路。看看一条实际地图上新的路对于整个交通的意义，就可以体会认知结构中这样一个新的联系的价值了。这个时候，概念地图还能够提示你在哪里建，怎么建这样一条新的道路。这个就是我们在上一小节结束的时候提到的：我们教和学的内容是用最少量最核心的概念和研究的例子以及它们之间的联系，来让学习者体会好这个学科的学科大图景，而所用的方法就是关注概念、研究工作、学科大图景之间的联系，让学习者自己来构建所学知识的概念地图，来体会学科大图景。并且这样的联系中，一定要关注内在联系，而不是牵强附会的联系。这个关注内在的联系而不是牵强附会的联系，我一会儿会分享一个例子，是批判性思维的一部分。因此，合起来，怎么学怎么教，就是靠“以学科大图景和成长型思维目标的以批判性思维和系联性思考为指导的以概念地图为技术基础的理解型学习”。

同时，这个概念地图可以用来反映概念地图制作者的认知结构，因此，这个制作概念地图的过程，在发现学习和理解中的问题，制订有针对性的个性化的学习方案中，也有着重要的作用。因此，概念地图也可以用于教学和学习的评价和诊断。由于概念地图的这个反映制作者的思考和理解的功能，在教学中，运用概念地图能够做到一定程度上个性化的教学。奥苏贝尔（David Ausubel） 在他的《教育心理学》 中说：

If I had to reduce all of educational psychology to just one principle, I would say this: The most important single factor influencing learning is what the learner already knows. Ascertain this and teach him accordingly。

如果非要我用一句话来概括教育心理学的原理，我会说：影响学习最重要的因素是学习者已经了解的东西。了解和考虑了这些东西以后来教。

因此，怎么学怎么教的问题就是两张地图的事儿：第一张，学科的核心知识的概念地图——这个学科的概念关系构成的概念地图是客观的，但是实际上呈现出来的学科专家或者授课老师所做的概念地图总是带有制作者的主观色彩的对这个客观关系的一种逼近；第二张，学生在相关知识上的已经有的概念地图——这个反映学生在学习阶段对这门学科的概念关系的把握。而且，后者需要在学习的过程中不断地更新。

在构建这张两概念地图的过程中，除了注意学科概念之间的联系之外，还需要注意概念和学科大图景之间的联系，也就是尽量选择那些能够体现学科大图景的概念、概念间联系来当做所要学习和理解的内容。这也就是我们提出[7]和提倡的学习方法：以学科大图景和成长型思维为目标的以批判性思维和系联性思考为指导的以概念地图为技术的理解型学习。

注：本文经授权选自吴金闪：《教的更少，学得更多——概念地图用于理解型学习》（科学出版社，2021年7月）。《返朴》发表时由于篇幅所限等原因，略有删改，本文题目为编者所加。有兴趣的读者可移步吴金闪教授个人微信公众号了解其更多内容。

注释

[1] 很多人都说，汤超的导师Per Bak ，也是沙堆模型的原创者之一，是一个具有非凡创造性的人。可惜，听不到Per Bak 关于这个问题的答案。如果你想了解这个具有非凡创造力的人更多，可以看看Per Bak 的书《大自然如何工作：有关自组织临界性的科学》。

[2] SageMath 是一个数学软件，可以做符号计算和数值计算。Sage: Open Source Mathematics Software， http://www.sagemath.org/ ， 2017 年 4 月 20 日访问。

[3] Maple 是一个数学软件，可以做符号计算。The Maple Software，http://www.maplesoft.com/， 2017年 4 月 20 日访问。

[4] 谷歌（Google）是一个搜索引擎， http://www.google.com/。

[5] Siri 是 一 个 语 音 控 制 系 统， 可 以 通 过 自 动 检 索 网 络 和 资 料 回 答 用 户 的 一 些 问 题。
https://www.apple.com/hk/en/ios/siri/。

[6] 关于具体定义和计算的理解的讨论，见吴金闪《教的更少，学得更多——概念地图用于理解型学习》 10.17 节，“秦磊、吴金闪：关于数学和科学理论与现实的关系以及学习方法的对话。”

[7] 不能说完全是我们提出的，其中各个部分独立来看，“成长型思维”“概念地图”“学科大图景”“批判性思维”“系联性思考”“理解型学习”，都是在我们之前就已经被提出来的。不过，把这几样东西合起来并且发展出来一个教和学的体系，就我所知，应该是我们提出来的。