[科普中国]-梅森公式

梅森公式，或称梅森增益公式，是在控制理论、自动化领域用于求取系统传递函数的公式。应用梅森公式将大大简化结构变换的计算，但当系统结构比较复杂时，很容易判断错误前向通道、回路、余子式的数目，因此常常将梅森公式和结构图变换结合起来用。也经常用两种方法互相验算。

相关概念系统传递函数线性定常系统的传递函数，定义为零初始条件下，系统输出量的拉氏变换与输入量的拉氏变换之比。2

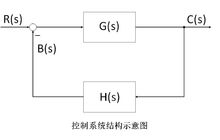
如对于典型的反馈系统，

有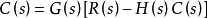

则经过整理，其传递函数为：

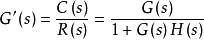
其中G(s)称为开环传递函数，G'(s)称为闭环传递函数；对于如图所示的系统，没有特殊声明，传递函数一般指闭环传递函数

结构图与信号流图为了抽象的表示系统，在控制领域中引入结构图以及信号流图两种常用形式来表示系统。

结构图，或形象的称为方框结构图，就是由许多对信号进行单向运算的方框和一些信号流向线组成的，其基本单元包括：信号线、引出点、比较点、方框。如上一节传递函数插图即为结构图。

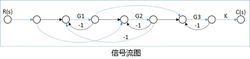
信号流图，起源于梅森利用图示描述一个或一组线性代数方程式，它是由节点和之路组成的一种信号传递网络。其中，节点标志系统的变量，支路相当于乘法器，信号只能沿箭头单向传递，给定系统的信号流图不唯一。2

公式由于结构图或信号流图都可以完整的表征整个系统，并且有着方便直观的化简方法，所以可以通过这两种图来求取系统的传递函数，但是当图过于庞大复杂，一点一点去化简就显得十分麻烦，为此在控制工程中常用梅森增益公式来直接求取系统的传递函数。

梅森公式如下2，

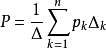
其中，

n——为前向通道总数；

P——系统总传递函数；

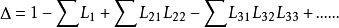，称为系统的特征式

pk——表示第k条前向通路的总增益；

△k——表示第k条前向通路的余因子式。3

参数详细说明特征式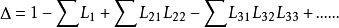

△ ——特征式中第二项表示所有单独回路增益之和，第三项表示每两个互不接触回路增益乘积之和，第四项表示每三个互不接触回路增益乘积之和，以此类推；

其中：

L1 —— 所有不同回路的传递函数之和；

L21L22 —— 所有两两不接触回路传递函数乘积之和（三个回路两两不接触不代表三个回路互不接触）；

L31L32L33 —— 所有三个互不接触回路传递函数乘积之和；

以此类推。

前向通路特征式的余子式△k——第k条前向通路特征式的余子式，即对于流图的特征式△，将与第k条前向通路相接触的回路

传递函数代以零值，余下的即为△k。3

回路传递函数回路传递函数是指反馈回路的前向通道和反馈通道传递函数的乘积，包含反馈极性的正、负号。

计算步骤①确定前向回路总数n；

②计算所有回路增益L；

③计算互不接触回路Lmn；

④计算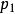 到 ；

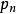⑤计算余子式△k；

⑥综合结果得到传递函数。

举例以上方信号流图为例(打开图片以查看)，

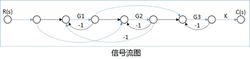
计算过程如下图所示，

①确定前向回路总数n=4；

②计算所有回路增益L

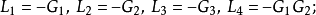
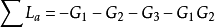
③计算互不接触回路

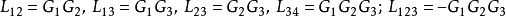
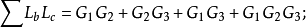
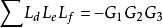
④计算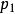 到

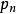
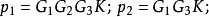
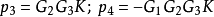
⑤计算余子式△k

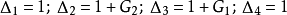
⑥综合结果得到传递函数

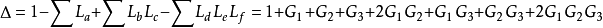
所以

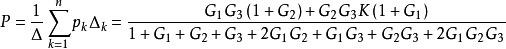
注意事项（1）n条前向通道数是指从输入信号至输出信号前向通道的总数，不要漏掉，不要重复，也不要错划。注意信号传递的单向性。

（2）单独回路数和互不接触回路数不要漏掉，亦不要重复。△和△k应计算无误。

（3）反馈的极性应体现在传递函数的正负上，一定要注意符号。

（4）梅森公式只能用于输入节点与输出节点之间。

本词条内容贡献者为:

齐臣杰 - 研究员 - 北京信息科技大学