[科普中国]-和角公式

和角公式又称三角函数的加法定理是几个角的和（差）的三角函数通过其中各个角的三角函数来表示的关系1。三角函数是数学中属于初等函数中的超越函数的一类函数。

诱导公式常用的诱导公式有以下几组:
1.sinα^2+cosα^2=1
2.sinα/cosα=tanα
3.tanα=1/cotα
公式一:
设α为任意角,终边相同的角的同一三角函数的值相等:
sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot(2kπ+α)=cotα
公式二:
设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
公式三:
任意角α与-α的三角函数值之间的关系:
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
公式四:
利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
公式五:
利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:
sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
公式六:
π/2±α及3π/2±α与α的三角函数值之间的关系:
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
(以上k∈Z)

三角函数和角公式一般的最常用公式有以下几组2：

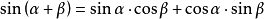
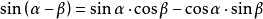
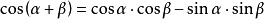
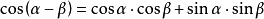
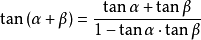
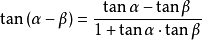
正弦余弦记忆口诀：正余同余正，余余反正正。

五个字代表右边的公式，“同”和“反”则表明中间的符号与左边是否一样；其中第一个字也代表是余弦公式还是正弦公式。

证明法一：向量证明

在平面直角坐标系中，以x轴为始边，作角α，角β，分别记其终边单位向量为a, b，则a=(cosα, sinα), b=(cosβ, sinβ)

∵**a****·**b=|a||b|cos

且**a****·**b=cosα·cosβ+sinα·sinβ

且|a|=|b|=1

∴cos=cos(α-β)=cosα·cosβ+sinα·sinβ

用-β代替β，得cos(α+β)=cosα·cosβ-sinα·sinβ

由诱导公式6，得sin(α-β)=-cos[(α-β)+π/2]=-cos[(α+π/2)-β]

=-[cos(α+π/2)·cosβ+sin(α+π/2)·sinβ]

=-[-sinα·cosβ+cosα·sinβ]

=sinα·cosβ-cosα·sinβ

同理得 sin(α+β)=sinα·cosβ+cosα·sinβ

又tan(α-β) = sin(α-β)/cos(α-β) = (sinα·cosβ-cosα·sinβ)/(cosα·cosβ+sinα·sinβ)

同除cosα·cosβ,得tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)

同理，tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)

证毕

法二：几何证明

下图α，β标识有误，建议放大观看。其中∠AOB应为α，∠AOP应为β。

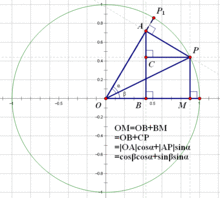cos(α-β)=OM

=OB+CP

=|OA|cosα+|AP|sinα

=cosα·cosβ+sinα·sinβ

适用范围和角公式是三角函数的一个基本公式，其实际应用有以下几个方面3：

1、其它三角公式的推导依据。

2、三角函数值的计算。

连同勾股定理，可以计算出各角度对应的函数值，是编制三角函数表的基本工具。

高等内容部分高等内容
高等代数中三角函数的指数表示
高等代数中三角函数的指数表示(由泰勒级数易得):
sinx=[e^(ix)-e^(-ix)]/(2i)
cosx=[e^(ix)+e^(-ix)]/2
tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]
泰勒展开有无穷级数,e^z=exp(z)=1+z/1!+z^2/2!+z^3/3!+z^4/4!+…+z^n/n!+…
此时三角函数定义域已推广至整个复数集。
三角函数作为微分方程的解
三角函数作为微分方程的解:
对于微分方程组y=-y'';y=y'''',有通解Q,可证明
Q=Asinx+Bcosx,因此也可以从此出发定义三角函数。
补充:由相应的指数表示我们可以定义一种类似的函数——双曲函数,其拥有很多与三角函数的类似的性质,二者相映成趣。

本词条内容贡献者为:

杨磊 - 副教授 - 北京大学数学学院