[科普中国]-换元法

解一些复杂的因式分解问题，常用到换元法，即对结构比较复杂的多项式，若把其中某些部分看成一个整体，用新字母代替(即换元)，则能使复杂的问题简单化，明朗化，在减少多项式项数,降低多项式结构复杂程度等方面有独到作用1。

换元法又称变量替换法 , 是我们解题常用的方法之一 。利用换元法 , 可以化繁为简 , 化难为易 , 从而找到解题的捷径 。

概述亦称辅助未知数法，又称变元代换法.解方程组的一种重要方法。它是普遍应用的一种方法，其一般意义是将由一个或几个变元构成的数学表达式中的一部分用新的变元表示，以利于问题的解决.这里仅给出在解方程(组)和解不等式(组)中的应用2。

它可以化高次为低次、化分式为整式、化无理式为有理式、化超越式为代数式，在研究方程、不等式、函数、数列、三角等问题中有广泛的应用。

分类换元法是指引入一个或几个新的变量代替原来的某些变量的变量求出结果之后，返回去求原变量的结果.换元法通过引入新的元素将分散的条件联系起来，或者把隐含的条件显示出来，或者把条件与结论联系起来，或者变为熟悉的问题.其理论根据是等量代换.

高中数学中换元法主要有以下两类：

(1)整体换元：以“元”换“式”。

(2)三角换元 ，以“式”换“元”。

(3)此外，还有对称换元、均值换元、万能换元等.换元法应用比较广泛。如解方程，解不等式，证明不等式，求函数的值域，求数列的通项与和等，另外在解析几何中也有广泛的应用。

整体换元又称整体换元，是在已知或者未知中，某个代数式几次出现，而用一个字母来代替它从而简化问题，当然有时候要通过变形才能发现。例如解不等式：4^x +2^x －2≥0，先变形为2^2x,设2^x =t（t>0），从而变为熟悉的一元二次不等式求解和指数方程的问题。

三角换元应用于去根号，或者变换为三角形式易求时，主要利用已知代数式中与三角知识中有某点联系进行换元。如求函数y=√1-x^2的值域时，若x∈[-1,1]，设x=sin α ，sinα∈[-1,1 ]，问题变成了熟悉的求三角函数值域。为什么会想到如此设，其中主要应该是发现值域的联系，又有去根号的需要。如变量x、y适合条件x^2+y^2 =r^2（r>0）时，则可作三角代换x=rcosθ、y=rsinθ化为三角问题。

均值换元如遇到x+y=2S形式时，设x= S+t，y= S－t等等。

例如清华大学自主招生考试题，已知a，b为非负实数，M=a^4+b^4，a+b=1,求M的最值

可令a=1/2-t,b=1/2+t(0≤t≤1/2),带入M，M=2×（t^2+3/4)^2-1，由二次函数性质知M（min)=1/8,M(max)=1.

等量换元设 x+y=3

x=t+2，y=v-3 ，多在二重积分中用到。

非等量换元设 u=（x+y）+3（x+y）

设x+y=S，也叫整体换元法。

应用技巧我们使用换元法时，要遵循有利于运算、有利于标准化的原则，换元后要注重新变量范围的选取，一定要使新变量取值范围对应于原变量的取值范围，不能缩小也不能扩大。如上几例中的t>0和sinα∈[-1,1 ]。

可以先观察算式，可发现这种需换元法之算式中总含有相同的式子，然后把它们用一个字母替换，推演出答案，然后若在答案中有此字母，即将该式带入其中，遂可算出3。

分解因式有时在分解因式时，可以选择多项式中的相同的部分换成另一个未知数，然后进行因式分解，最后再转换回来，这种方法叫做换元法。

相关例题注意:换元后勿忘还元。

【例】在分解(x²+x+1)(x²+x+2)-12时，可以令y=x²+x,则 原式=(y+1)(y+2)-12 =y²+3y+2-12=y²+3y-10 =(y+5)(y-2) =(x²+x+5)(x²+x-2) =(x²+x+5)(x+2)(x-1)．

例2，(x+5)+(y-4)=8

(x+5)-(y-4)=4

令x+5=m,y-4=n

原方程可写为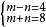

解得m=6,n=2

所以x+5=6,y-4=2

所以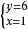

特点：两方程中都含有相同的代数式，如题中的x+5,y-4之类，换元后可简化方程。

解高次方程

有时在解方程时，可以选择方程中的相同的部分换成另一个未知数，达到降次的目的，然后进行新方程求新未知数，最后再转换回来求原未知数，这种方法叫做换元法。

相关例题注意:换元后勿忘还元。

【例】解方程（x²-2x）²-3（x²-2x）-4=0

解：设x²-2x=y，则原方程变为y²-3y-4=0

(y-4)(y+1)=0

y-4=0或y+1=0

y1=4 y2=-1

当y=4时，x²-2x=4 解得x1=1+√5 x2=1-√5

当y=-1时，x²-2x=-1解得x1=x2=1

所以，原方程的根为x1=1+√5 x2=1-√5 x3=1

二重积分的换元法定理 设f(x,y)在x0y平面上的闭区域D上连续，变换T：x=x(u,v),y=y(u,v)，将u0v平面上的闭区域D'变为x0y平面上的D，且满足

（1）x(u,v)，y(u,v)在D'上具有一阶连续偏导数；

（2）在D'上雅可比式

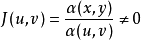
（3）变换 T：D'→D是一对一的，

则有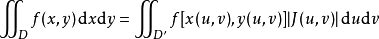

上边的公式称为二重积分的换元公式。4

本词条内容贡献者为:

郎奠波 - 副教授 - 黑龙江财经学院