定义
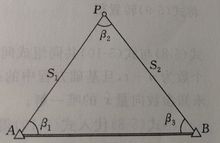
以观测方程作为函数模型的平差方法,称为间接平差法。如图1所示边角网,有5个观测值,必要观测数t=2。如果选择P点坐标作为2个独立参数,则可以列出所有观测方程。
例如,S1边和角度β1的观测方程为
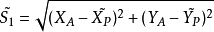
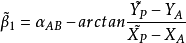
实际上,如果在这些方程中,将观测值的期望值用观测值本身来代替的话,这些方程之间将产生矛盾。平差的目的就是合理地消除这些矛盾。1
设在测量系统中有n个观测值L,又选择了t个独立参数,观测方程的一般形式可表示为
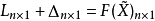
线性化形式为
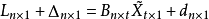
上式可写成
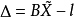
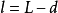
如果将真值△和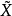 用估值V和
用估值V和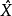 代替,则有
代替,则有

上式称为误差方程。间接平差法的随机模型为已知观测值的方差及相关信息。
原理间接平差法可以列出n个如下平差值线性方程。
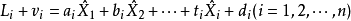
设
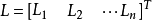
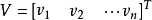
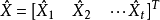
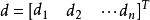

则平差值方差可以写成矩阵形式为
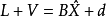
设
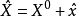
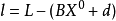
即参数平差值由近似值X0和改正数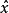 构成,则矩阵形式可变为
构成,则矩阵形式可变为
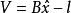
参数的解算应满足条件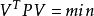 。问题变为求极值问题,将
。问题变为求极值问题,将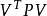 对
对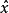 求导,并令其为零得
求导,并令其为零得
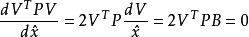
转置得
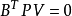
上式与参数平差值的矩阵形式共同组成间接平差的基础方程。基础方程共有(n+t)个,方程中的未知量个数为n+t,且基础方程中的系数阵均为满秩阵,因此,可以由基础方程得到改正数向量V和未知参数向量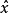 的唯一解。
的唯一解。
求解基础方程得
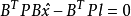
设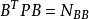 ,
,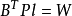 ,则上式可简写为
,则上式可简写为
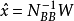
或写为
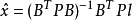
综合以上公式,可得到改正数向量V的解,从而得到观测值及参数的平差值为
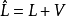
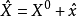
过程与步骤(1)在测量系统中,选择t个独立参数,其个数应与必要观测数相同。参数的选取具有较大的自由度,如可以使得所选参数为有用值,且使得建立误差方程较为容易;
(2)列出误差方程,并将其线性化;
(3)根据实际应用情况,确定观测值的权;
(4)由误差方程的系数阵及常数项,组成法方程的系数阵及常数项阵;
(6)由误差方程计算观测值改正数向量V,并求出观测值的平差值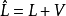 。
。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国