[科普中国]-椭球扁率

定义

为了解决在大地水准面这个复杂曲面上进行数据处理的困难问题，在测绘工作中常选用一个表面非常接近大地水准面、并且可以用数学模型表达的几何形体来代替地球的几何形状1，此几何形体通常称为地球椭球体，又称旋转椭球体。

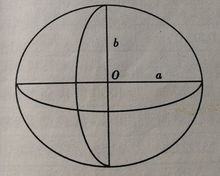
地球椭球是控制测量中用以代表地球的椭球，通常简称椭球，它是地球的数学代表。地球椭球体形状及大小通常由子午椭圆的五个基本几何参数（或称元素）来决定，包括椭圆的长半轴a，短半轴b，椭圆扁率、椭圆的第一偏心率和第二偏心率。其中椭球的扁率公式为

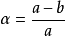
性质扁率α反映了椭球体的扁平程度。当a=b时，α=0，此时椭球体变为球体；当b减小时，α增大，则此时椭球体变扁；当b=0时，α=1，则变为平面。因此，扁率的大小由椭球的长半轴与短半轴共同决定，且其值介于1和0之间。

当把地球看作圆球时，地球大气呈球对称分布，大气折射中心与地球的球心重合；而当考虑椭球扁率影响时，折射中心相对于地球椭球中心有了偏移。为了改正由于扁率带来的偏差，折射角与影响参数的计算应该相对于折射中心。2因此，椭球扁率对各项研究带来的误差等影响，是不容忽视的。

应用传统大地测量利用天文大地测量和重力测量资料推求地球椭球的几何参数。从19世纪以来，已经求出许多地球椭球参数。3较著名的有：①克拉索夫斯基椭球体，其扁率规定为1/298.3；②1975年国际椭球体，规定扁率为1/298.257；③WGS-84椭球体，规定扁率为1/298.257223563；④2000中国大地坐标系（CGCS2000），规定其为1/298.257222101。

在地质历史上的变化下限利用地球扁率，将地球假设为弹性椭球体，根据弹性动力学理论推导出扁率下限公式。扁率与地球平均密度、引力加速度、自转角速度、平均半径、弹性模量等均相关。根据地质历史时期半径、质量、角速度等变化值可计算出各地质历史时期的椭球扁率值4，从而作为扁率变化值的下限，用以研究地球形状的长期变化。

子午线弧长公式简化子午线弧长计算是经典大地测量问题之一，因子午线弧长问题涉及椭圆积分，不能直接求出，其经典算法是按二项式定理展开的级数展开。为提高收敛速度，国际上多以椭球的扁率来进行代换。利用椭球扁率进行对子午线弧长公式的简化，丰富了子午线弧长的理论与应用。5

对引潮力位的影响固体潮广泛用于地球物理、空间科学与地震监测研究，而引潮力位（TGP）调和展开是固体潮研究与分析计算中的基本理论问题，也是潮汐观测分析与研究工作的基础6。关于TGP调和展开，有频谱分析法与解析演绎法，其展开精度已能满足重力观测和空间测地技术的需要，但根据位理论与微积分方法，还可导出顾及地球扁率的TGP表达式。从引力潮位出发，通过对外界天体在地球质心处产生引力、进行受力分析的研究，并基于空间直角坐标系转换方法，可推导出椭球扁率对TGP的表达式，从而产生对引力潮位的重新讨论。