[科普中国]-几何定向

几何定向特点

定向精度：与起始方位精度和观测仪器等级有关。

实时性：需观测传递方位的多个转折角，无法做到实时性。

自主性：完全自主。

受外界影响：受外界条件影响很多，如大风会影响仪器的稳定，地而辐射热会影响大气的稳定，大气透明度会影响照准精度，温度变化会影响仪器的正常状态等。

成本：成本低。

功能：获取坐标方位2。

一井定向在一个立井中自由悬挂两根钢丝垂线，由地面向井下传递平面坐标和方向的测量工作。如图，在井筒中自由悬挂两根钢丝垂线A、B，它代表一个铅垂面，利用该面上的任一条直线都具有相同的方位角和垂线上任一点的平面坐标都相同的原理，将地面平面坐标和方向传递到井下。一井定向工作，除定向投点和井上、下连接测量外，还需进行地面连测导线测量，以求得地面连接测量的起算数据1。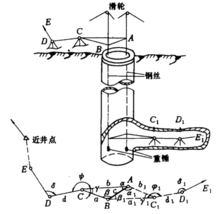

地面连测导线测量地面由近井点至连接点的导线称为地面连测导线。定向之前，必须在地面井口附近设立作为定向时与钢丝垂线连接的点C(井下为C1)，称为连接点。由近井点开始测设地面连测导线，以求出连接点C的坐标及连接边CD的坐标方位角，作为地面连接测量的起算数据。中国《煤矿测量规程》规定的精度要求为：测角中误差不超过±5″，导线全长相对闭合差不超过1/10000。对小煤矿，可适当放宽要求1。

定向投点定向投点可用钢丝投点或激光铅垂仪投点。中国广泛采用钢丝投点。用钢丝投点时，钢丝上端固定在地面，下端(在定向水平上)悬挂重锤(垂球)，并将重锤放入水桶中，以减少钢丝垂线的摆动。

钢丝投点方法分为单重投点和多重投点。

单重投点法，是在投点的过程中，垂球的重量保持不变。多重投点法则是在投点的过程中，利用改变垂球的重量来确定地面钢丝垂线点在定向水平上的正确位置。单重投点法较之多重投点法作业简单，效率高，得到广泛应用。单重投点法又分为单重稳定投点和单重摆动投点两种。前一种是将垂球(重锤)放在水桶中，使其静止，在定向水平上就与静止的钢丝垂线进行连接测量。后一种是用经纬仪观测垂线的自由摆动以确定其稳定位置，并加以固定，在定向水平上就与此固定的钢丝垂线进行连接测量。垂线的摆幅很小能基本静止时，采用稳定投点，否则须采用摆动投点1。

由于井筒内气流、滴水等的影响，钢丝垂线在地面的位置投到定向水平后会发生偏离，这种线量偏差称为投点误差。由投点误差引起的两垂线连线的方向误差，叫做投向误差。投向误差 θ 按下式计算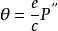：，式中 e 为钢丝投点误差，m；c 为两垂线间的距离，m；ρ″=206265″ 为每弧度的角秒数。

两垂线间的距离 c 受井筒直径的限制，一般为4m左右，因而由投点误差引起的投向误差是很大的，成为一井定向误差的主要来源。为此，减少投点误差的措施为：定向时停止风机运转或增设风门，以减少风速；在井下采用防风套筒套着垂线，以隔离风流对钢丝的作用；采用直径小、抗拉强度高的钢丝，适当加大重锤的重量，并将重锤放入稳定液中。此外，应尽量增大两垂线间的距离，以减少投向误差1。

连接测量连接测量工作可采用三角形连接法、瞄直法和四边形法。

**三角形连接法：**以连接点和井筒中两垂线构成延伸三角形(图1的ΔABC和ΔABC1)进行一井定向的连接测量方法，是一种应用广泛的地面与井下连接测量方法。

(1)三角形图形要求。从连接测量误差尽量小的观点出发，c边愈长，a/c(或a1/c)、γ(或γ1)角愈小的延伸三角形是最有利的连接图形。

(2)施测。地面连接测量时，在C点测量水平角γ、φ；用钢尺精确丈量a、b、c三边长。井下连接测量时，同法测量γ1、φ1角度和三角形三边长度。此外，井上下还须分别测量δ、δ1角及d、d1边长。

(3)计算。地面和井下垂线处不能直接测量的角度α、β和α1、β1。

(4)定向误差估算。为设计定向工作，需对定向误差进行估算。

**瞄直法：**又名穿线法。如图2，用瞄线法将地面连接点C与井下连接点C1分别设置在两垂线A、B的延长线上，即C-A-B-C1位于同一竖直平面内。在C与C1点安置经纬仪测出角度φ、φ1，量出CA、AB和BC1的长度，就能按导线D-C-C1-D1计算出井下C1点的坐标和C1D1边的坐标方位角1。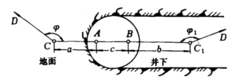

四边形连接法：井下连接测量的一种方法。当受井口、井筒和井底车场的条件限制，必须在与两垂线连线的大致垂直方向连接时，采用此法。如图3，井下连接点P1、P2与两垂线A、B构成四边形。根据两已知点A、B来确定两未知点P1、P2的平面坐标及其连线的坐标方位角1。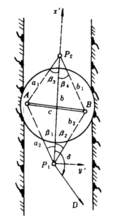

两井定向在有井下巷道相连通的两个立井中各挂一根钢丝垂线由地面向井下传递平面坐标和方向的测量工作。如图4，在两个立井中各挂一根钢丝垂线A、B，由地面控制点K敷设导线测定两垂线的坐标，在井下两垂线间敷设经纬仪导线，经计算将地面平面坐标及方向传递到井下。两井定向工作包括定向投点，井上、下连接测量及其计算。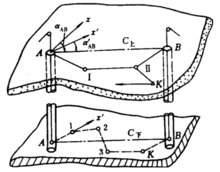

地面连接测量地面连接测量的目的在于测定两钢丝垂线的坐标。由近井点K向两垂线A、B测设连接导线K-Ⅱ-Ⅰ-A及K-Ⅱ-B，算出两垂线的坐标xA、yA及xB、yB。

井下连接测量在井下定向水平，沿两井间相通的巷道测设井下经纬仪导线A-1-2-3-4-B。以垂线A的地面坐标为起算数据，根据井下导线各边的坐标方位角和边长计算井下导线各点的坐标，完成定向任务。

测量和计算的检查用比较井上与井下算得的两垂线间距离c上和c下进行检查。

两井定向与一井定向相比，投点误差对定向精度的影响大大减小，连接测量作业简单，占用井筒时间少，定向精度高1。

经纬仪进行几何定向简介在传统测量中，无论是测角网、测边网、边角网，还是附合导线、闭合导线和支导线的布设，通过角度测量传递已知方位是确定地面点位的基本测量工作之一，常用的角度测量仪器有经纬仪、全站仪。由于单从角度测量而言，经纬仪与全站仪等价，故此以经纬仪为例叙述2。

要通过经纬仪实现定向功能，确定出地面任意两点连线的坐标方位，必须具备已知起始数据：一已知坐标方位或两已知坐标，故该定向法误差包含有已知起始方位误差，其次是水平角观测误差。在水平角观测误差中有各种各样的误差来源，其中误差来源不同对水平角观测的精度也有着不同的影响，主要包括五方面的误差来源：1)仪器误差；2)仪器对中误差；3)目标偏心误差；4)照准误差与读数误差；5)外界条件的影响。其中仪器误差有属于制造方面的，如水平度盘偏心与刻划误差、水平度盘与竖轴不垂直等；有属于校正不完善的，如竖轴与照准部水准管轴不完全垂直，视准轴与横轴的残余误差。至于仪器对中误差和目标偏心误差均属于“对中”性质的误差，就对中本身而言是偶然误差，可是一旦目标标志和仪器已经安置，则对中误差的真值不再发生变化，因此该误差在一次架站中又具有系统性。另外，读数误差主要是针对光学经纬仪而言的，取决于仪器的读数设备，而电子数显经纬仪则不存在该误差2。

对于水平角观测精度，通常以某级经纬仪的标称精度作为基础，应用误差传播定律进行分析。设某级经纬仪室外一测回方向中误差为m1方，则一测回角值中误差为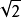m1方，如按 n 测回观测水平角，则m角=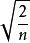m1方。故几何定向法的精度可表示为：m定=m起+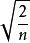m1方2。