[科普中国]-折射角

折射角简介

1.光的折射定律：三线同面，法线居中，空气中角大，光路可逆。

﹙1﹚折射光线，入射光线和法线在同一平面内。

﹙2﹚折射光线和入射光线分居在法线两侧。

﹙3﹚光从空气斜射入水或其他介质中时，折射角小于入射角，当入射角增加时，折射角随着增加。光从水中或其他介质斜射入空气中时，折射角大于入射角．当光从空气垂直射入（或其他介质射入），传播方向不改变。

2.光的折射规律总结：

（1）三线一面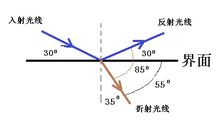

（2）两线分居

（3）两角关系分三种情况：

①入射光线垂直界面入射时，折射角等于入射角等于0°；

②光从空气斜射入水等介质中时，折射角小于入射角；

③光从水等介质斜射入空气中时，折射角大于入射角。

3．应用：从空气看水中的物体，或从水中看空气中的物体看到的是物体的虚像，看到的位置比实际位置高。

折射定律折射定律的数学表达式为：sini:sinγ=v1：v2

i是入射角，γ是折射角，v1，v2是两种介质中的光速。

又因真空中的光速c最大且恒定，故规定

n=c/v，n就是折射率。

显然，有

sini:sinγ=v1:v2=n2/n11

相关推导用费马原理推导费马原理又称为“最短时间原理”：光线传播的路径是需时最少的路径。费马原理更正确的版本应是“平稳时间原理”。对于某些状况，光线传播的路径所需的时间可能不是最小值，而是最大值，或甚至是拐值。例如，对于平面镜，任意两点的反射路径光程是最小值；对于半椭圆形镜子，其两个焦点的光线反射路径不是唯一的，光程都一样，是最大值，也是最小值；对于半圆形镜子，其两个端点Q、P的反射路径光程是最大值；又如最右图所示，对于由四分之一圆形镜与平面镜组合而成的镜子，同样这两个点Q、P的反射路径的光程是拐值。

假设，介质1、介质2的折射率分别为n1、n2，光线从介质1在点O传播进入介质2，θ1为入射角，θ2为折射角。

从费马原理，可以推导出斯涅尔定律。通过设定光程对于时间的导数为零，可以找到“平稳路径”，这就是光线传播的路径。光线在介质1与介质2的传播速度分别为v1=c/n1，v2=c/n2。其中，c为真空光速。

由于介质会减缓光线的速度，折射率n1、n2都大于1。

如右图所示，从点Q到点P的传播时间为

.

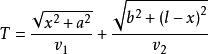
根据费马原理，光线传播的路径是所需时间为极值的路径，取传播时间T对变量x的导数，并令其为零。经整理后，可得dT/dx=sinθ1/v1-sinθ2/v2=0。

将传播速度与折射率的关系式代入，就会得到折射定律：n1sinθ1=n2sinθ2。2

用麦克斯韦电磁场理论推导由于光波是某个特定频段的电磁辐射，因此光必须满足麦克斯韦方程组与伴随的边界条件。其中一条边界条件为，在边界的临近区域，电场平行于边界的分量必须具有连续性。假设边界为xOy平面，则在边界，有

E∥，i(x，y，0)+E∥，r(x，y，0)=E∥，t(x，y，0)。

其中，E∥，i、E∥，r、E∥，t分别为在入射波、反射波、折射波（透射波）的电场平行于边界的分量。

假设入射波是频率为ω的单色平面波，则为了在任意时间满足边界条件，反射波、折射波的频率必定为ω。

设E∥，i、E∥，r、E∥，t的形式为

E∥，i=E∥，i0exp(iki·r-ωt)，

E∥，r=E∥，r0exp(ikr·r-ωt)，

E∥，t=E∥，t0exp(ikt·r-ωt)。

其中，ki、kr、kt分别是入射波、反射波、折射波的波矢量，E∥，0、E∥，r0、E∥，t0分别是入射波、反射波、折射波的波幅（可能是复值）。

为了在边界任意位置（x，y，0）满足边界条件，相位变化必须一样，必须设定

kixx+kiyy=krxx+kryy=ktxx+ktyy。

因此，kix=krx=ktx，kiy=kry=kty。

不失一般性，假设kiy=kry=kty=0，则立刻可以推断第一定律成立，入射波、反射波、折射波的波矢量，与界面的法线共同包含于入射平面。

从波矢量x分量的等式，可以得到

kisinθi=krsinθr。

而在同一介质里，有ki=kr，

于是，第二定律成立，入射角θi等于反射角θr。

应用折射率的定义式：n=c/v=ck/ω，

可以推断第三定律成立：nisinθi=ntsinθt。

其中，nt、θt分别是折射介质的折射率与折射角。

从入射波、反射波、折射波之间的相位关系，就可以推导出几何光学的三条基础定律。

一般来说：对同一束光，θ2空气中>θ2玻璃中>θ2水中。