[科普中国]-施瓦尔兹不等式

数学上，柯西-施瓦茨不等式，又称施瓦茨不等式或柯西-布尼亚科夫斯基-施瓦茨不等式，是一条很多场合都用得上的不等式；例如线性代数的矢量，数学分析的无穷级数和乘积的积分，和概率论的方差和协方差。它被认为是最重要的数学不等式之一。它有一些推广，如赫尔德不等式。

不等式以奥古斯丁·路易·柯西（Augustin Louis Cauchy），赫尔曼·阿曼杜斯·施瓦茨（Hermann Amandus Schwarz），和维克托·雅科夫列维奇·布尼亚科夫斯基（Виктор Яковлевич Буняковский）命名。1

柯西-施瓦茨不等式叙述，对于一个内积空间所有向量x和y，

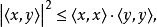其中 表示内积，也叫点积。等价地，将两边开方，引用向量的范数，不等式可写为

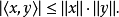
另外，等式成立当且仅当x和y线性相关（或者在几何上，它们是平行的，或其中一个向量的模为0）。

若 和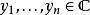 有虚部，内积即为标准内积，用拔标记共轭复数那么这个不等式可以更明确的表述为

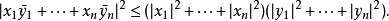
柯西—施瓦茨不等式的一个重要结果，是内积为连续函数，甚至是满足1阶利普希茨条件的函数。2

对欧几里得空间Rn，有

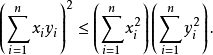等式成立时：

也可以表示成

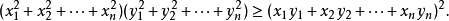
证明则须考虑一个关于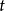 的一个一元二次方程式 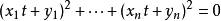，很明显的，此方程式无实数解或有重根，故其判别式 。

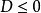注意到

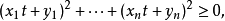
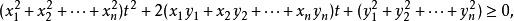
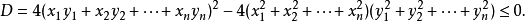即

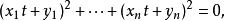
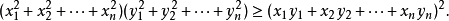而等号成立于判别式 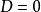时，也就是此时方程式有重根，故

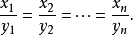
对平方可积的复值函数，有

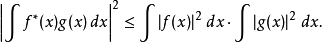这两例可更一般化为赫尔德不等式。

在3维空间，有一个较强结果值得注意：原不等式可以增强至拉格朗日恒等式

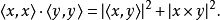这是

在n=3 时的特殊情况。3

设在区域D及其边界上解析，为D内一点，以为圆心做圆周，只要及其内部G均被D包含，则有：

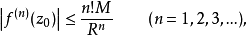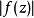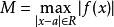其中，M是的最大值，。4

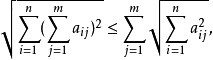
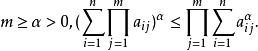
三角不等式

内积空间