[科普中国]-上三角行列式

主对角线(从左上角到右下角这条对角线)下方的元素全为零的行列式称为上三角行列式。一个n阶行列式若能通过变换，化为上三角行列式，则计算该行列式就很容易了。

基本介绍三角形行列式(triangular determinant)是一种特殊的行列式，数域P上形如

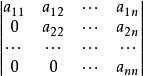或

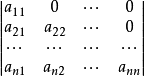的行列式分别称为上三角形行列式和下三角形行列式，亦称上三角行列式和下三角行列式，统称三角形行列****式。每个行列式都可以只运用行或者列的性质化为一个与其相等的上(下)三角形行列式。上(或下)三角形行列式都等于它们主对角线上元素的乘积。行列式

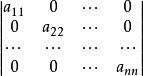称为对角形行列式，亦称对角行列式。它既是一个上三角形行列式，又是一个下三角形行列式1。

行列式的七条性质1. 行列式D与它的转置行列式相等。

2. 互换行列式的两行(列)，行列式的值改变符号。

由性质2可得出：如果行列式有两行(列)的对应元素相同或成比例，则这个行列式为零。

3. n阶行列式等于任意一行(列)的所有元素与其对应的代数余子式的乘积之和。即

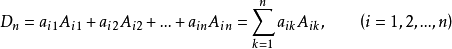或

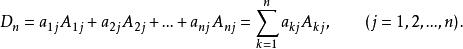
性质3说明了行列式可按任一行或任一列展开。一般地，如果行列式的某一行或某一列中零元素较多；则按该行或该列展开来计算行列式会简便一些。

4.n阶行列式中任意一行(列)的所有元素与另一行(列)的相应元素的代数余子式的乘积之和等于零。即当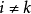时有

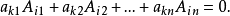由性质3和性质4，可得到如下结论：

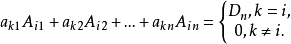
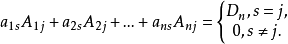
5.行列式某一行(列)的公因子可以提出来。即用一个数乘行列式就等于用这个数乘行列式的某一行或某一列。

6.如果行列式中某- 一行(列)的元素可写成两数之和，则这个行列式等于两个行列式的和，而且这两个行列式除了这一行(列)以外，其余的元素与原行列式的对应元素相同。

7. 将行列式的某一行(列)的各元素都乘以同一个常数后，再加到另一行(列)的对应元素上，其值不变2。

化行列式为上三角行列式利用以下三条性质，可以把所给n阶行列式化为上三角行列式，从而算出这个行列式的值。

(1) 互换行列式中某两行(或某列)位置，行列式前乘(-1)；

(2) 行列式中某行(或某列)有公因子，这个公因子可以提到行列式外面去；

(3) 把行列式的某一行(或某一列)的任意倍加到另一行(或另一列)上去，行列式的值不变3。

例1计算四阶行列式

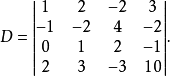
解： 利用上述行列式的第三条性质，把第一行的1倍加到第二行上去，再把第一行的(-2)倍加到第四行上去

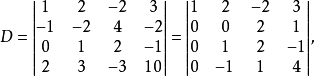(再互换第二行和第三行的位置)：

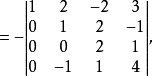(将第二行的1倍加到第四行上去)：

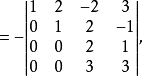(第四行提出公因子3后与第三行互换位置)：

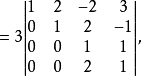(将第三行的-2倍加到第四行上去)：

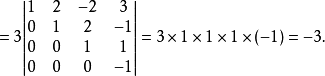
本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学