[科普中国]-近似平差

近似平差配合全站仪不仅可以直接测量距离和角度，也可以直接进行坐标测量，给测量工作带来极大方便。应用全站仪附合导线坐标测量的近似平差计算方法，并对点位的精度进行分析，为提高测量精度，采用从起始点及终点分别向中间点进行推测的办法，可以极大减低中间点（最弱点）的误差，提高测量精度。

概念近似平差一般都是配附。以附闭合导线为例，近似平差是先测方位角闭合差，在闭合差符合规范要求的情况下先配附角度，然后计算坐标，在坐标差值合格相对全长精度合格的情况下，在配附坐标。一般来说在测图作业，工程测量作业等项目上，是完全可行的。

卡西欧fx-4800P计算器附合导线近似平差程序研究背景附合导线近似平差是工程施工测量中经常要做的工作。工程开工前，需要对业主委托测绘部门提供的原始控制导线点进行复测，然后按监理单位提供的表格将观测数据、计算过程数据、复测平差结果等报监理审批。在原始控制点的基础上，根据施工控制需要布置施工控制导线，对测量结果进行平差计算也是必不可少的工作。这些工作以前或是在夏普1500、E500袖珍机上进行，或是手工进行，但前者已逐渐退出市场，后者又比较繁琐易出错。

可编程计算器已普遍应用于工程测量工作中，卡西欧fx-4800p程序计算器即是其中的一种。它较fx-4500在内存上有了大幅度提高，共有4500字节容量，具有体积小，重量轻，携带方便，多行显示，存储量大等诸多优点，可满足一般工程测量计算需要。但它又不同于夏普1500、E500，在变量、内存使用方面受到限制，将附合导线近似平差程序移植到它上面需要些技巧。笔者在实际工作中将附合导线平差程序移植到了卡西欧fx-4800p计算器上，现将其介绍如下，以供同行参考。

附合导线近似平差程序如图1所示，附合导线起点A，起始方位角为α0，终点B，终点方位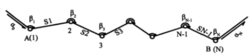角为αN，左角观测值为β1、β2…βN，边长观测值S1、S2…SN-1。

角度闭合差及其分配：

fβ=α0+∑β-N*180-αN

Vβ=-fβ/N

计算改正方位角：

αi=αi-1+βi+Vβ-180；i=1…N

坐标增量计算：

ΔXi=cosαadb *Si；i=1…N

ΔYi=sinαi*Si；i=1…N

坐标闭合差计算及精度评定：

fx=XA+∑ΔX-XB

fy=YA+∑ΔY-YB

fS=√(f2x +f2y)

k=fS/∑S

坐标增量改正数计算：

VΔXi=-fx/∑S*Si；i=1…N-1

VΔYi=-fy/∑S*Si；i=1…N-1

计算导线点坐标：

Xi+1=Xi+ΔXi+VΔXi；i=1…N-1

Yi+1=Yi+ΔYi+VΔYi；i=1…N-1

研究结论卡西欧fx-4800p程序计算器是近年来出现的一种较为先进的程序计算器，一般市政工程施工测量内业计算工作它都能胜任。本文仅仅介绍了它在附合导线近似平差中的应用。其更多应用，还有待于广大测量工作者结合实际工作去不断地开发。1

附合导线测量近似平差方法及点位精度分析与传统光学测量仪器相比，全站仪最大的特点就是便捷、高效，能代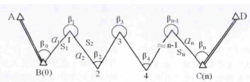替测距仪进行斜距自动测量，代替经纬仪进行竖直角、水平角的测量，且能自动记录、计算并显示出相关数据。此外，全站仪还能通过内置的程序功能完成对边测量、三维坐标测量等复杂的测量工作，给测量工作带来方便，广泛应用于测量的各个领域。2

测量原理与方法全站仪导线测量是指利用全站仪通过内置的程序功能对地面点进行的坐标测量，见图2。

如图2所示，A、B、C、D为已知高级控制点，1、2、3、…、n-1等为加密控制点。测量时与边角导线基本相同，全站仪安置在i点，观测i+1点的坐标。首先将全站仪安置在已知点B，输入B点的坐标和高程HB，量仪器高i、棱镜高v，并瞄准另一相邻已知点A进行定向，照准目标点1上的反射棱镜进行测量，全站仪可利用仪器至反射棱镜的斜距S，仪器至反射棱镜的竖直角以及测站点B至目标点1的方位角α自动按照公式计算并显示出B点与1点之间的水平距离D以及1点的坐标和高程。全站仪三维坐标测量实质是利用极坐标的方法测定目标点的平面坐标，用三角高程测量方法测定目标点的高程。1点测量结束后，将1点作为新测站，B点作为后视点，同法可以继续测定2点的坐标，直至测量结束。由此观测过程容易看出，全站仪坐标测量实际上坐标只测量半个测回，高程为单向观测，为提高精度，测量时可以采用正倒镜观测和双向观测的方法。

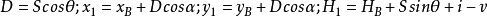
导线的近似坐标平差传统的附合导线测量转折角和边长，平差方法有近似方法和严密方法。近似平差方法的基本思想是角度测量误差不影响边长，边长测量误差不影响角度，所以平差时将角度和边长单独平差，该方法计算简单，但显然不符合实际，所以精度会受影响。严密平差方法的基本思想是边长和角度测量的误差都会对角度和边长产生影响，平差时将角度和边长的误差一起考虑，加以计算，该方法符合实际，但计算工作复杂，计算量大。

采用坐标法进行导线近似平差，直接在已经测得导线点的坐标上进行改正，方法简单，易于掌握，避免了传统近似平差法的方位角的推算和改正，以及坐标增量的计算和改正，能大大提高工作效率，而且不易出错。同时，传统附和导线测量需要两条已知边，作为方位角的检核条件，而直接坐标法，只需要一条已知边和一个已知点即可，使导线的布网更加灵活。

研究结论综上分析，点离起点越远精度越低，为提高测量精度，采用从起始点及终点分别向中间点进行推测的办法，可以极大地减低中间点（最弱点）的误差，提高测量精度，或者理解为在精度要求不变的前提下，可以延长一倍导线长度。同时，提高边长测量精度，需要特别注意对中、照准误差的限制。3

本词条内容贡献者为:

张磊 - 副教授 - 西南大学