屏蔽常数是原子中其它电子对某一特定电子屏蔽核引力程度的量度。
引出根据量子力学中心力场模型,多电子原子中某单电子i的近似原子轨道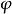 对应能级
对应能级 可表示为:
可表示为:
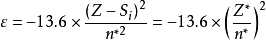
同时引入屏蔽效应和屏蔽常数、有效核电荷、有效主量子数等概念。Slater于1930年,提出一套判定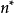 、
、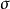
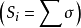 大小的规则,曾得到广泛应用。之后,许多人从不同角度讨论它,通过不同途径修正它。后来确定了的
大小的规则,曾得到广泛应用。之后,许多人从不同角度讨论它,通过不同途径修正它。后来确定了的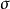 值大小的规则,即不下十余种。概括起来可分为两类:
值大小的规则,即不下十余种。概括起来可分为两类:
第一类以Slater、徐光宪为代表,他们先后对光谱实验结果进行分析总结,得到Slater规则和徐光宪规则。
第二类的代表是shibuya,他修正Slater轨函数为目的,认为有效量子数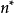 的引入方便,仍采用主量子数
的引入方便,仍采用主量子数 ,通过量子力学的理论分析,给出一套屏蔽常数
,通过量子力学的理论分析,给出一套屏蔽常数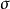 的取值规则。
的取值规则。
这两类规则,对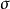 的赋值有很大的不同。1
的赋值有很大的不同。1
近似赋值斯莱特(Slater)经验规则是最经典的近似地计算屏蔽常数的规则,其要点如下:
将原子中电子按下列顺序分成若干轨道组:1S2、2S2 2P6;3S2 3P6、3d10;4S2 4P6、4d1-10、4f1-14;5S2 5P6……并注明每组电子数目,所有这些电子对原子中某一特定电子的屏蔽效应的总和,可用屏蔽常数的加和求算之。
分布在特定电子外面的电子不发生屏蔽效应,即屏蔽常数 s=0。
在特定电子组的电子,除特定电子外,其它每个电子的屏蔽常数为0.35(1s 组电子的屏蔽常数为0.30。
在紧邻特定电子所在层的较内电子层(n-1)层中,每个电子的屏蔽常数为0.85。
比(n-1)电子层更靠近原子核的各电子层中,每个电子的屏蔽常数为1.00。
如果特定电子是在d或f亚层中,则分布在较低电子组中每个电子的屏蔽常数为1.00。
斯莱特规则的核心是通过有效核电荷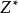 和有效主量子数
和有效主量子数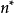 两个经验参数来计算多电子原子中某一指定原子轨道的能量。若知道了屏蔽常数,就可以计算有效核电荷以及多电子原子中各原子轨道的能量。2
两个经验参数来计算多电子原子中某一指定原子轨道的能量。若知道了屏蔽常数,就可以计算有效核电荷以及多电子原子中各原子轨道的能量。2
应用计算原子的各级电离能为了计算院子的各级电离能,通常采用Slater公式:
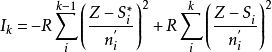
式中:Ik为相应于失去k电子的第K级电离能,Z为核电荷,ni'为i电子的有效主量子数,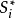 和
和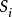 为K价和K-1价正离子中各电子对i电子屏蔽常数之总和。3
为K价和K-1价正离子中各电子对i电子屏蔽常数之总和。3
解释过渡元素的基电子组态和电离态用屏蔽常数规律可以解释过渡元素的基电子组态和电离态,例如铬元素的基电组态是[Ar]3d54S1。4
本词条内容贡献者为:
李雪梅 - 副教授 - 西南大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国