[科普中国]-逐次线性化

逐次线性化是指若目标函数及约束条件在某一个可行点附近线性化后得出的解点仍然保持在可行域之内，则在这一解点附近重新将目标函数及约束条件进行线性化，得出并求解新的线性规划问题。如此继续下去，当逐次得出的解点都保持在可行域内时，则可望这些解点能逐次逼近原非线性规划问题的极小点的方法。

计算方法目标函数及约束条件在某一个可行点附近线性化后得出的解点，则在这一点附近将函数或者约束条件进行线性化。1

当解点超出可行域范围时，增加一个限制步长的约束条件，计算中每次迭代所用的步长可以先取用前次迭代的数值，若解点超出可行域则减少这一数值重新求解该线性规划问题，直到满足收敛要求并得出极值点。

步长限值的取值对算法的成功与否有很大影响，由于一般都采用较小的步长，所以又称小步长梯度法。实践证明这种方法在目标函数为凸函数且可行域为凸集的情况下是收敛的，然而其确切的收敛性能尚未得到充分证明。另外这种方法所需要的迭代次数通常比较多，计算工作量也比较大，且花费的时间也比较多。

示例假设有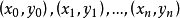在数值逼近学科中，拉格朗日插值能够得到n次插值多项式，然而，每当有新的节点增加， 原来的计算出的数据均不能利用，需要重新计算，为了克服这个缺点，提出了逐次线性化插值法，由于插值多项式的存在唯一，利用逐次线性插值求出的插值多项式和拉格朗日插值多项式相同。2

通过这些点做逐次线性插值，其大体思想如下：

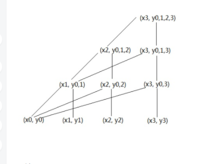
迭代公式：

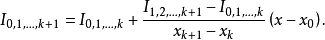
本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学