[科普中国]-孤立元素

对于一个集合A，当x∈A时，若有x-1不∈A，并且x+1不∈A，则称x为A的一个孤立元素。

概念对于一个集合A，当x∈A时，若有x-1不∈A，并且x+1不∈A，则称x为A的一个孤立元素。例如集合S={1,2,3,5,7}，5和7是孤立元素，因为4，6，8不属于集合S或集合B={5,7,9,10}，5和7是孤立元素，因为4，6，8不属于集合B。

集合集合（简称集）是数学中一个基本概念，它是集合论的研究对象，集合论的基本理论直到19世纪才被创立。最简单的说法，即是在最原始的集合论——朴素集合论中的定义，集合就是“确定的一堆东西”。集合里的“东西”，叫作元素。

由一个或多个确定的元素所构成的整体叫做集合。若x是集合A的元素，则记作x∈A。集合中的元素有三个特征：1.确定性（集合中的元素必须是确定的）。 2.互异性（集合中的元素互不相同）。例如：集合A={1，a}，则a不能等于1）。 3.无序性（集合中的元素没有先后之分），如集合{3,4,5}和{3,5,4}算作同一个集合。

元素集合是指具有某种特定性质的具体的或抽象的对象汇总成的集体，这些对象称为该集合的元素。

例如全中国人的集合，它的元素就是每一个中国人。我们通常用大写字母如A,B,S,T,...表示集合，而用小写字母如a,b,x,y,...表示集合的元素。若x是集合S的元素，则称x属于S，记为x∈S。若y不是集合S的元素，则称y不属于S，记为y∉S。一般的我们把含有有限个元素的集合叫做有限集，含无限个元素的集合叫做无限集。

集合分类空集有一类特殊的集合，它不包含任何元素，如{x|x∈R x²+1=0} ，我们称之为空集，记为∅。

空集是个特殊的集合，它有2个特点：

空集∅是任意一个非空集合的真子集。

空集是任何一个集合的子集。

子集设S，T是两个集合，如果S的所有元素都属于T ，即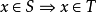则称S是T的子集，记为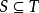。显然，对任何集合S ，都有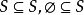。其中，符号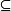读作包含于，表示该符号左边的集合中的元素全部是该符号右边集合的元素。

如果S是T的一个子集，即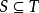，但在T中存在一个元素x不属于S ，即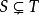，则称S是T的一个真子集。

相等如果两个集合S和T的元素完全相同，则称S与T两个集合相等，记为S=T 。显然我们有

其中符号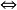称为当且仅当，表示左边的命题与右边的命题相互蕴含，即两个命题等价。1

并交集并集定义：由所有属于集合A或属于集合B的元素所组成的集合，记作A∪B（或B∪A），读作“A并B”（或“B并A”），即A∪B={x|x∈A,或x∈B}。并集越并越多。

交集定义：由属于A且属于B的相同元素组成的集合，记作A∩B（或B∩A），读作“A交B”（或“B交A”），即A∩B={x|x∈A,且x∈B}。交集越交越少。

若A包含B，则A∩B=B，A∪B=A。

补集相对补集定义：由属于A而不属于B的元素组成的集合，称为B关于A的相对补集，记作A-B或A\B，即A-B={x|x∈A，且x∉B'}。

绝对补集定义：A关于全集合U的相对补集称作A的绝对补集，记作A'或∁u（A）或~A。有U'=Φ；Φ'=U。

幂集定义：设有集合A，由集合A所有子集组成的集合，称为集合A的幂集。

定理：有限集A的幂集的基数等于2的有限集A的基数次幂。

区间数学分析中，最常遇到的实数集的子集是区间。

设a，b(a