最大线性无关组也称为极大线性无关组,是代数中线性相关与线性无关中的基本概念。极大线性无关组表示一组向量中,由最多个线性无关的向量组成的部分,并且从这一向量组中任意添一向量,这个部分组就线性相关。
定义1向量组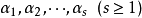 称为线性相关,如果有数域
称为线性相关,如果有数域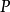 中不全为零的数
中不全为零的数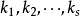 ,使得
,使得
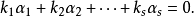
定义2一向量组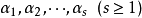 不线性相关,即没有不全为零的数
不线性相关,即没有不全为零的数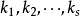 ,使得
,使得
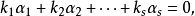 就称为线性无关;或者说,一向量组
就称为线性无关;或者说,一向量组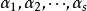 称为线性无关,如果由
称为线性无关,如果由
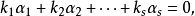 就可以推出
就可以推出
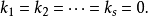 换个说法,如果一向量组线性无关,那么它的任何一个非空的部分组也线性无关。特别地,由于两个成比例的向量是线性相关的,所以,线性无关的向量组中一定不能包含两个成比例的向量。
换个说法,如果一向量组线性无关,那么它的任何一个非空的部分组也线性无关。特别地,由于两个成比例的向量是线性相关的,所以,线性无关的向量组中一定不能包含两个成比例的向量。
定义3一个向量组的一部分组称为一个极大线性无关组1,如果这个不分组本身是线性无关的,并且从这向量组中任意添一向量(如果还有的话),所得的部分向量都线性相关。
例如,在向量组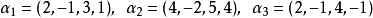 中,由
中,由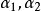 组成的部分组就是一个极大线性无关组。首先,
组成的部分组就是一个极大线性无关组。首先,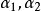 线性无关,因为由
线性无关,因为由
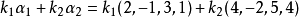
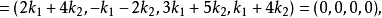
就有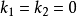 。同时我们知道,
。同时我们知道,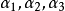 线性相关。不难看出,
线性相关。不难看出,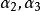 也是一个极大线性无关组。
也是一个极大线性无关组。
应该看到,一个线性无关向量组的极大线性无关组就是这个向量组本身。
极大线性无关组的一个基本性质是,任意一个极大线性无关组都与向量组本身等价。
事实上,设向量组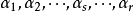 ,而
,而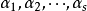 是它的一个极大线性无关组。所谓等价就是它们可以互相线性表出。因为
是它的一个极大线性无关组。所谓等价就是它们可以互相线性表出。因为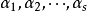 是
是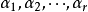 的一部分,当然可以被这个向量组线性表出,即
的一部分,当然可以被这个向量组线性表出,即
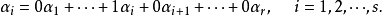 因此,问题在于
因此,问题在于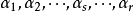 是否可以被
是否可以被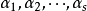 线性表出。向量
线性表出。向量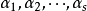 中每一个都可以被
中每一个都可以被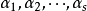 线性表出是显然的。再来看
线性表出是显然的。再来看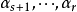 中的向量,设
中的向量,设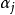 是这样一个向量,由极大线性无关组
是这样一个向量,由极大线性无关组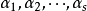 的极大性,向量组
的极大性,向量组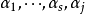 线性相关,也就是说,有不全为零的数
线性相关,也就是说,有不全为零的数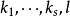 使得
使得
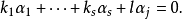 因为
因为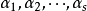 是线性无关的,可证必有
是线性无关的,可证必有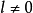 。否则,设
。否则,设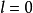 ,那么
,那么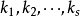 就不全为零,于是
就不全为零,于是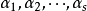 线性相关,这与假设矛盾。由
线性相关,这与假设矛盾。由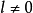 ,上式可以改写为
,上式可以改写为
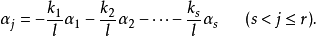 这就是说,
这就是说,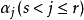 可以被
可以被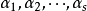 线性表出。于是证明了向量组与它的极大线性无关组的等价性。
线性表出。于是证明了向量组与它的极大线性无关组的等价性。
由上面的例子可以看出,向量组的极大线性无关组不是惟一的。但是每一个极大线性无关组都与向量组本身等价,因而,一向量组的任意两个极大线性无关组都是等价的。
定理1一向量组的极大线性无关组都含有相同个数的向量。
定理1表明,极大线性无关组所含向量的个数与极大线性无关组的选择无关,它直接反映了向量组本身的性质。
定义4向量组的极大线性无关组所含向量的个数称为这个向量组的秩。
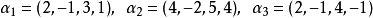 例如,向量组的秩就是2。
例如,向量组的秩就是2。
因为线性无关的向量组就是它自身的极大线性无关组,所以一向量组线性无关的充分必要条件为它的秩与它所含向量的个数相同。
我们知道,每一向量组都与它的极大线性无关组等价。由等价的传递性可知,任意两个等价向量组的极大线性无关组也等价。所以,等价的向量组必有相同的秩。
还要指出:含有非零向量的向量组一定有极大线性无关组,且任一个无关的部分向量组都能扩充成一个极大线性无关组。全部由零向量组成的向量组没有极大线性无关组,规定这样的向量组的秩为零。
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国