波德图(英语:Bode plot,“Bode”的英文发音类似Boh-dee,荷兰文的发音则类似Bow-dah),又名伯德图、波特图,是线性非时变系统的传递函数对频率的半对数座标图,其横轴频率以对数尺度表示,利用波德图可以看出系统的频率响应。波德图一般是由二张图组合而成,一张幅频图表示频率响应增益的分贝值对频率的变化,另一张相频图则是频率响应的相位对频率的变化。
波德图可以用电脑软件(如MATLAB)或仪器绘制,也可以自行绘制。利用波德图可以看出在不同频率下,系统增益的大小及相位,也可以看出大小及相位随频率变化的趋势。
波德图的图形和系统的增益,极点、零点的个数及位置有关,只要知道相关的资料,配合简单的计算就可以画出近似的波德图,这是使用波德图的好处。
简介波德图是由贝尔实验室的荷兰裔科学家亨德里克·韦德·波德在1930年发明。波德用简单但准确的方法绘制增益及相位的图,因此他发明的图也就称为波德图。
波德图幅频图的频率用对数尺度表示,增益部分一般都用功率的分贝值来表示,也就是将增益取对数后再乘以20。由于增益用对数来表示,因此一传递函数乘以一常数,在波德增益图只需将图形的纵向移动即可,二传递函数的相乘,在波德幅频图就变成图形的相加。幅频图纵轴0分贝以下具有正增益裕度、属稳定区,反之属不稳定区:
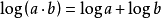
波德图相频图的频率也用对数尺度表示,而相位部分的单位一般会使用度。配合波德相频图可以估算一信号进入系统后,输出信号及原始信号的比例关系及相位。例如一个Asin(ωt) 的信号进入系统后振幅变原来的k倍,相位落后原信号Φ,则其输出信号则为(Ak)sin(ωt−Φ),其中的k和Φ都是频率的函数。相频图纵轴-180度以上具有正相位裕度、属稳定区,反之属不稳定区
若将系统的增益以复数表示,则复数增益取对数后的虚部即为相位,因此二传递函数的相乘,在波德相位图上也是图形的相加。
波德图的增益和相位很难单独的变动、二者会互相牵扯,当调整系统的增益响应时,系统的相位响应也会随之变化,反之亦然。最小相位系统的增益和相位特性之间可以用希尔伯特转换来转换,因此知道其中一项即可求出另外一项。
若转换函数是有理函数,其零点及极点均为实数,则其波德图可以用几条渐近线的直线来近似,利用简单的规则即可以徒手绘制。若近似的波德图再修正每个截止频率时的增益值,则其近似值会更接近实际值。1
波德图手绘的规则波德图的前提就是可以处理以下型式函数的对数值:
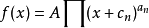
上述函数的对数值可以转换为极点及零点对数的和:
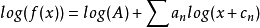
在绘制波德相位图时直接使用了上述的概念。增益图的绘制时则是以此概念为基础,因为每个极点或零点其增益的对数均从0开始,而且其渐近线只有一个转折点,因此绘制时可以再作简化。
直线近似的增益图波德图增益分贝值一般都利用 20log10(X)的公式。考虑以下的转换函数:
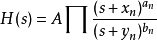
其中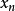 及
及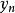 是常数,s=jΩ,an,bn>0,而H是转换函数。
是常数,s=jΩ,an,bn>0,而H是转换函数。
在每个对应{\displaystyle \omega =x_{n}}(零点)的位置,将直线的斜率增加{\displaystyle 20\cdot a_{n}\ dB}/十倍频。
在每个对应{\displaystyle \omega =y_{n}}(极点)的位置,将直线的斜率减少{\displaystyle 20\cdot b_{n}\ dB}/十倍频。
图在起始点时的增益值,可以依照图中的角频率下限,计算其对应的|H(jω)|。
图在起始点时的斜率则依照有多少零点及极点低于角频率下限,再依上述二个方式计算斜率,若所有点及极点均高于角频率下限,起始点时的斜率为零。
在处理无法分解的二次多项式{\displaystyle ax^{2}+bx+c\ }时,多半可以用{\displaystyle ({\sqrt {a}}x+{\sqrt {c}})^{2}}的方式近似。
波德图(Bode)是振动的幅值(尤指工频分量或二阶分量)和相位随转速而变化的图。与频响函数的幅、相频特性曲线类似。从波德图上可以清楚的看出转子过临界转速的振动状况。
波德图(bode)是反映机器振动幅值、相位 随转速变化的关系曲线。图形的横坐标是转速,纵坐标有两个,一个是振幅的峰-峰值,另一个是相位。从波德图上我们可以得到以下信息:
随转速变化的关系曲线。图形的横坐标是转速,纵坐标有两个,一个是振幅的峰-峰值,另一个是相位。从波德图上我们可以得到以下信息:
a. 转子系统在各种转速下的振幅和相位;
b. 转子系统的临界转速;
c. 转子系统的共振放大系数(Q=Amax/ε);一般小型机组Q在3~5甚
至更小,而大型机组在5~7;超过上述数值,很可能是不安全的;
d. 转子的振型;
e. 系统的阻尼大小;
f. 转子上机械偏差和电气偏差的大小;
g. 转子是否发生了热弯曲。2
稳定性一般是指作用在系统上的扰动排除后,系统能否恢复原状、或以怎样的精度恢复原状的性能。它是控制理论的一个极其重要的问题。在经典控制理论中,一般涉及到的是定常的线性系统,有关这种系统的稳定性的判别方法主要有: 罗斯—胡尔维茨准则、奈奎斯特判据、波德图、尼柯尔图和根轨迹法等。在现代控制理论中,对线性系统和非线性系统的稳定性的研究,主要是李雅普诺夫的稳定性理论。李雅普诺夫根据系统的输出 (响应) 是否有界来定义系统的稳定性,并区分了三种情况: (1) 稳定的,即对于系统初始值的一个扰动,如果其响应的幅值是有界的。(2) 渐近稳定的,即对于系统初始值的一个扰动,如果其响应能够最终回到初始状态。(3)不稳定的,即对于系统初始值的一个扰动,其响应的幅值不是有界的。经典控制理论所研究的稳定性只限于第二种情况渐近稳定,而把另两种情况都看作是不稳定的。因而李雅普诺夫的稳定性概念更具一般性。李雅普诺夫用两种方法分析系统的稳定性,第一种方法是: 用近似极数表示非线性函数,然后用近似方法求解非线性方程,最后根据解的性质,确定其系统的稳定性; 第二种方法是: 不必求解方程,而用李雅普诺夫函数的纯量函数来判别系统是否稳定,并分析系统的响应。由于第二种方法具有不必求解方程的特点,因而也称直接法,而称第一种方法为间接法。由于许多非线性系统和时变系统的方程是难以求解的,又由于通过计算机可以找到所需的李雅普诺夫函数,还能找到系统的稳定区域,所以第二种方法在控制理论中得到广泛应用。稳定性对于社会经济系统极为重要,是经济学经常讨论的重要课题之一。探讨经济系统的稳定性,对于了解经济系统的动态发展规律、预测经济发展方向以及分析经济系统的结构等,都有着重要的现实意义。3
本词条内容贡献者为:
李雪梅 - 副教授 - 西南大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国