[科普中国]-内切球

球心到某几何体各面的距离相等且等于半径的球是几何体****的内切球。如果一个球与简单多面体的各面或其延展部分都相切，且此球在多面体的内部，则称这个球为此多面体的内切球。与圆柱两底面以及每条母线都相切的球称为这个圆柱的内切球，此圆柱称为球的外切圆柱。与圆台的上、下底面以及每条母线都相切的球，称为圆台的内切球，此圆台称为球的外切圆台1。

多面体的内切球如果一个球与简单多面体的各面或其延展部分都相切，且此球在多面体的内部，则称这个球为此多面体的内切球(inscribed sphere of a polyhedron)。多面体称为这个球的外切多面体，正多面体的内切球均存在，正多面体内任意点到各面距离之和为常数

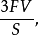这里F为多面体的面数，S为表面积，V为体积，故正多面体内切球半径为。

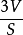圆柱的内切球与圆柱两底面以及每条母线都相切的球称为这个圆柱的内切球(inscribed sphere in a circular cylinder)，此圆柱称为球的外切圆柱，等边圆柱才有内切球，球心在圆柱轴线中点处，内切球半径与圆柱底面圆半径相等。

圆锥的内切球与圆锥的底面和各母线均相切的球，称为圆锥的内切球(inscribed sphere in a circular cone)，此圆锥称为球的外切圆锥。圆锥的内切球有且仅有一个，球心在圆锥的轴线上，当圆锥高为h，底面圆半径为r时，则内切球半径

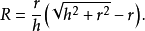
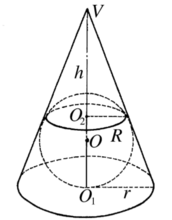
圆台的内切球与圆台的上、下底面以及每条母线都相切的球，称为圆台的内切球(inscribed sphere in a frustum of a circular cone)，此圆台称为球的外切圆台，当且仅当母线长与上、下两底面圆半径之和相等时，圆台才有内切球1。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学