[科普中国]-斜圆柱

斜圆柱的表面积

圆柱的全面积是刻画圆柱表面积大小的一个数量及其计算公式。直****圆柱的侧面积与底面积的和为它的全面积。如果直圆柱的底面半径为r，高为h，那么它的全面积为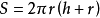 。斜圆柱的侧面积和它的两底椭圆面积的和是它的全面积。设母线长为l，直截面网周长为C，底面椭圆的长短半轴为a、b，斜圆柱全面积为 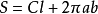。1

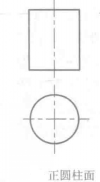
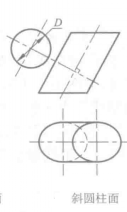
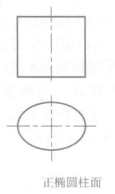
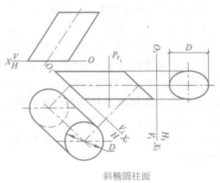
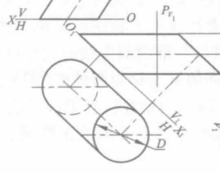
斜圆柱的正截面与柱面轴线垂直的截平面称为正截面，如图10一10所示．正截面与柱面的截交线(称正****截交线)为圆，则柱面为圆柱面(回转圆柱面)，圆柱面的轴线垂直于圆柱底面时，称为正圆柱****面。如图10一10a所示。圆柱面的轴线倾斜于圆柱底面时，称为斜圆柱面，图10一lOb所示的斜圆柱底面形状为椭圆，如正截交线为椭圆，则称为椭圆柱面，椭圆柱面的轴线垂直于柱底时，称为正椭圆柱面，如图10一l0ce所示。椭圆柱面的轴线倾斜于椭圆柱底面时，称为斜椭圆****柱面，如图10—10d所示。

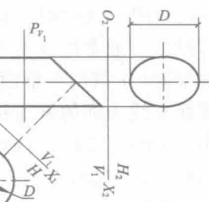
正截面与柱面截交线的实形可用变换投影面法求得。如图10一lOd所示，作一垂直于轴线的正截面P，平面P与柱面的交线实形为椭圆(其长轴等于导圆的直径D)，因此这个柱面为椭圆柱面。2

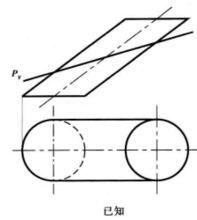
求平面与斜圆柱的截交线例1 求平面P与斜圆柱的截交线(素线法)，如图4(a)所示。

解：分析：斜圆柱被正垂面P切割。斜圆柱的柱面的V、H投影无积聚性，故其截交线上的一般点的求解只能用素线法来求解。

作图：如图4(b)所示。

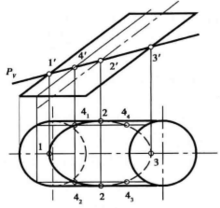
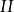①求特殊点：求椭圆长、短轴的端点 和 (前后两条素线上的特殊点都以 点表示)。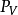 与圆柱正面投影轮廓素线的交点1’、3’，是椭圆长轴端点 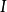、 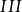的正面投影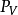； 与圆柱最前、最后素线的正面投影的交点为2’，由此求出长短轴端点的水平投影1、2(注意前后共有两个点)、3。

②求一般点：为使作图准确，还需要再求出属于截交线的若干个一般点。例如在截交线正面投影上任取一点4'。4’是椭圆上一般点的正面投影，我们采用对称的方式来求解Ⅳ点在H面4个位置上的投影。根据椭圆是对称图形，可作出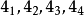 四个点。

③连点：在H投影面上用光滑的曲线依次连接各点，即得截交线的水平投影。

判别可见性：由图可知截交线以短轴为分界线，左半部分为可见，右半部分为不可见。3

斜圆柱体的展开1) 做出斜圆柱的主视图。把斜圆柱两边素线点标为A、C、B、D（见图5,图5(b)、(c)是图5(a)的放大图）。

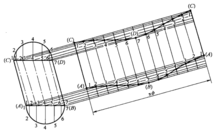
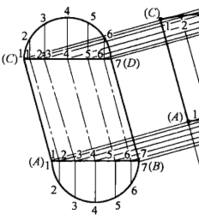
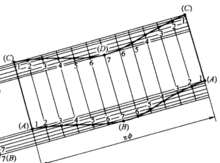
2) 分别做斜圆柱上端线段AB和下端线段CD的半圆，并把半圆六等分，过上下两半圆等分点做垂线，上半圆等分点垂线垂直于线段CD，下半圆等分点垂线垂直于线段AB，在线段CD与线段AB上对应得交点1、2、3、4、5、6、7点。用线段把上下1、2、3、4、5、6、7点对应相连。

3) 过斜主视图上下1、2、3、4、5、6、7点向右引十四条平行线，平行线与斜圆柱素线AC与BD垂直。截取上边1点平行线的长等于斜圆柱圆的周长，并做十二等分，过等分点做平行线的垂线，与十四条平行线对应相交，上下同时对应得交点为1、2、3、4、5、6、7、6、5、4、3、2、1点。用曲线分别把上下的交点顺次圆滑相连，即得到斜圆柱的展开图。4