[科普中国]-岭估计

基本介绍

在多重共线性下，由于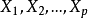之间存在着较高的线性相关关系，导致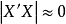，因此设想给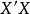加上一个正常数矩阵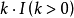，那么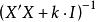接近奇异的可能性要比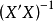接近奇异的可能性小甚至小很多，所以用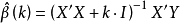作为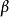的估计要比普通最小二乘法所得到的估计量稳定，这就是所谓的岭估计。

岭估计方法的目的主要是减少均方误差，提高估计量的稳定性，但其缺点是估计量是有偏的。可以看到，k值越大，估计量的方差就越小；同时，k的引入也会使最小二乘估计量的无偏性发生变化，变成有偏估计量，k越大，偏误也就越大。而一个好的估计量应该是无偏的、方差最小的估计量，由于这两个标准是相互矛盾的，因此k的确定就会变得很困难。到目前为止，虽然许多专家学者已提出多种确定k值的方法，但是，还没有一种大家公认的、最优的确定k值的方法。3

k值确定方法

下面仅针对岭估计方法，介绍几种常用的k值确定方法。

岭迹法

岭估计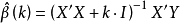的分量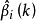作为k的函数，当k在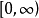之间变化时，在平面直角坐标系中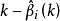所描绘的图像称为岭迹曲线。我们可以根据岭迹曲线的变化形状来确定适当的k。常用的岭迹曲线及其显示出的相关特点如下：

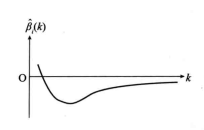
1) 在图1(a)中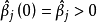，，并且比较大。这时可以将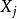看做是对Y有重要影响的因素。但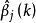的图形不稳定，当k从零开始略增加时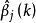，显著地下降，而且迅速趋于零，从岭回归的观点看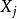，对Y不起作用。

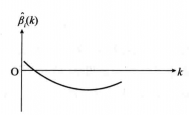
2) 与图1(a)相反的情况如图1(b)所示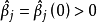，，但很接近零，这时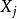对Y的作用不大，但是随着k略增加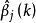，骤然变为负值，从岭回归观点看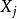，对Y有显著的影响。

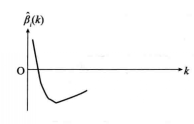
3) 在图1(c)中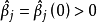，，说明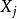还比较显著，但当k增加时，迅速下降，且稳定为负值，这时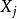是对Y有重要影响的显著因素，从岭回归分析的角度看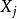，对Y有负影响的因素。

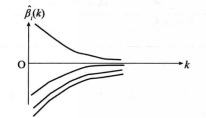
4) 在图1(d)中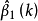，和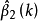都很不稳定，但其和却大体稳定。这种情况往往发生在自变量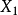和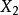的相关性很大的场合，即在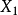和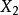之间存在多重共线性的情形，从选择自变量的角度，两者只保存一个就够了。这种情况可以解释某些回归系数估计的符号不合理的情形，从实际观点看，和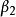不应有相反符号。

5) 从全局看，岭迹分析可用来估计在某一具体问题中最小二乘估计是否适用，把所有回归系数的岭迹都绘制在一张图上，如果这些曲线比较稳定，如图1(e)所示，利用最小二乘估计会有一定的把握。3

利用岭迹法可以确定k，一般确定k需要遵循下面几个原则：

1) 回归方程各回归系数的岭估计基本稳定；

2) 用普通最小二乘法估计时，正负号表现出不合理的回归系数，而利用岭估计其符号变得合理，即岭估计方法的使用改善了回归方程参数估计的效果；

3) 回归系数没有出现不合理的符号；

4)估计量的精度没有降低太多，即残差项的平方和增大得不太多。3

方差扩大因子法

在识别多重共线性时，我们了解了方差扩大因子的概念，其可以用于度量多重共线性关系的严重程度，一般，当方差扩大因子>10时，模型的多重共线性关系就严重影响到估计量的质量。如果计算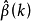的协方差，得

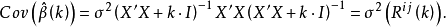则此式中矩阵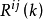的对角元素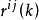就是岭估计的方差扩大因子。不难看出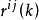，随着k的增大而减少。应用方差扩大因子选择k的经验做法是，选择使所有方差扩大因子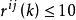的k．这样的k会使得岭估计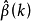相对稳定。

此外，还可以根据Hoerl、Kernard和Baldwin(1975)提出的方法取k的固定值。具体确定方法如下：对于标准化的回归模型

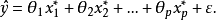k的计算公式是

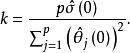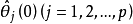其中，为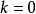时回归模型参数的最小二乘估计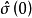，为回归方程的残差均方。3

迭代法

迭代法是将上面计算的k的固定取值作为k的初始值，记为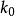，然后建立回归方程，估计回归方程的参数，并计算新的k，即：

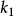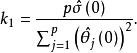按同样的方法，用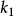计算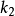，重复这一过程，直到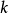的前后两个估计值之间的差异不是很明显为止。3