定义定义一
置信系数又称“置信概率”、“置信度” “信度系数”。系区间估计中,使估计的总体参数落在置信区间的概率,即式
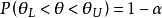 中的
中的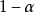 ,式中的
,式中的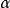 则称为置信水平。置信系数
则称为置信水平。置信系数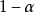 表示估计正确的概率,一般为95%或95%以上,置信水平
表示估计正确的概率,一般为95%或95%以上,置信水平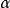 表示参数估计不准的概率,一般为5%或5%以下。上式则意味着,若反复抽样多次(每次样本容量相等),每组样本观察值确定一个区间(
表示参数估计不准的概率,一般为5%或5%以下。上式则意味着,若反复抽样多次(每次样本容量相等),每组样本观察值确定一个区间(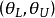 ),每个这样的区同要么包含
),每个这样的区同要么包含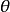 的真值,要么不包含
的真值,要么不包含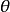 的真值,其
的真值,其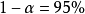 则指出,这样多的区间中,包含真值的约占95%,不包含真值的则仅占5%。2
则指出,这样多的区间中,包含真值的约占95%,不包含真值的则仅占5%。2
定义二在应用概率的方法估计实验误差时,经常使用置信系数这个概念,它的定义是:遵从一定概率分布的某项误差对应于所给置信概率的误差限与标准差之比,叫做该项误差的置信系数。若用K表示置信系数,e表示误差限,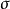 表示标准差,则有定义的数学表达式
表示标准差,则有定义的数学表达式
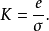
从物理意义上来理解,就是说一项误差的概率分布确定之后,标准差即确定,对应于所给置信概率(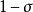 )的误差限也就确定了,该误差限可以用标准差乘以一个系数来表示,这个系数就是置信系数。
)的误差限也就确定了,该误差限可以用标准差乘以一个系数来表示,这个系数就是置信系数。
可见,置信系数是描述对于某一个置信概率情况下标准差和误差限(或置信限)之间关系的一个量,它的大小不但与置信概率有关,而且与概率分布有关。3
置信系数的计算如果已经知道被测量的均方响应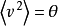 的概率密度
的概率密度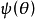 ,那么落在置信区间
,那么落在置信区间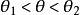 内的概率——置信系数
内的概率——置信系数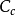 可写为:4
可写为:4
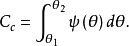
若不知道具体的函数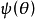 ,但知道
,但知道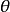 可能是正值,并可估算
可能是正值,并可估算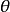 的平均值
的平均值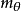 和它的标准偏差
和它的标准偏差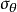 此时可利用伽马
此时可利用伽马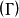 分布函数,形成均方响应
分布函数,形成均方响应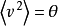 的概率密度函数
的概率密度函数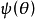 为:
为:
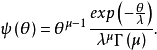 式中
式中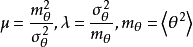 作变量替换:
作变量替换:
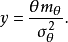 代入
代入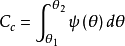 式可得:
式可得:
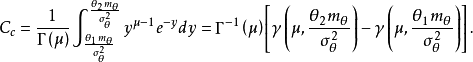 式中
式中
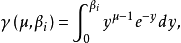 式中
式中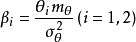 通常可从数学手册中查表得到上述有关的函数值。4
通常可从数学手册中查表得到上述有关的函数值。4
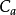 与
与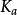 的区别
的区别
在误差合成中,往往运用广义方和根法来计算总不确定度u,即
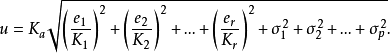
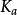 为
为 个未定系统误差及p个随机误差之和的概率分布的置信系数(
个未定系统误差及p个随机误差之和的概率分布的置信系数(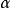 为显著性水平,一般取
为显著性水平,一般取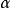 =0.01)。
=0.01)。
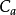 特指误差概率分布为正态分确时的置信系数,对应置信概率为(1一
特指误差概率分布为正态分确时的置信系数,对应置信概率为(1一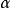 ),(一般取
),(一般取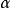 =0.01)。
=0.01)。
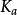 随误差之和的概率分布不同而取不同的值,特别,当误差之和遵从(或接近于)正态分布时,
随误差之和的概率分布不同而取不同的值,特别,当误差之和遵从(或接近于)正态分布时,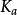 即可采用
即可采用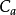 的数值。
的数值。
置信系数在误差合成中的作用置信系数在误差合成中有较大的作用,主要为以下两方面:
i)对于各项未定系统误差,利用各自概率分布的置信系数,可以很方便地进行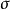 与e之间的换算,有利于采用较好的广义方和根法进行误差合成。
与e之间的换算,有利于采用较好的广义方和根法进行误差合成。
ii)对于已求得的标准差,乘以置信系数即可得到不确定度(或误差限),置信系数选得过大,误差限就大干客观误差限,显得保守;反之就冒险,因此,应该根据误差的概率分布和需要的置信概率来合理选取。使误差合成结果尽可能符合实际情况。3




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国