[科普中国]-射影坐标

基本概述射影

射影是物体在某平面或某空间形成的投影。

射影几何射影几何是研究图形的射影性质，即它们经过射影变换后，依然保持不变的图形性质的几何学分支学科。曾经也叫做投影几何学，在经典几何学中，射影几何处于一个特殊的地位，通过它可以把其他一些几何学联系起来。1

射影坐标这里主要介绍以点为基本元素的平面上的射影坐标系，其他二维基本形或其他维的基本形上的射影坐标系与此相仿。 建立射影坐标系的方法很多，一般说来有几何方法和解析方法。

建立方法建立射影坐标系的方法很多，一般说来有几何方法和解析方法。

几何方法它以射影几何的基本不变量交比为基础。

解析过程

设在射影平面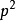 上取四点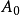 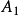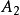， ， 和E，其中每三点不共线；前三点叫做射影坐标系的基点，E叫做幺点(单位点)。 设p为 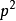上任意点，作交比

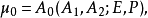
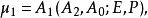
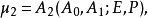式中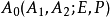 表示四条直线 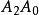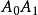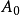， ， E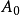， p 的交比，其余两式相仿。不难证明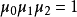， 。于是可以令：

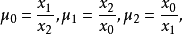
而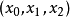 就是p点的齐次射影坐标。 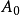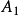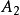， ， 和E的坐标依次是 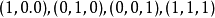。在射影坐标系里,任意直线的方程是含 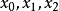的线性齐次方程。特殊地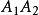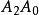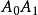， ， ， 的方程依次是 。

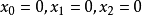若用扩大欧氏平面或扩大仿射平面代替射影平面，通过上述方法所得的就是扩大平面上的射影坐标系。在欧氏平面或仿射平面上，先建立笛卡儿坐标系，则在扩大平面上的齐次笛卡儿坐标系可以看作扩大平面上一种特殊的射影坐标系，其基点是笛卡儿坐标系的原点和两条坐标轴上的无穷远点，而幺点则是具有非齐次坐标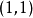 的点。

在射影直线p上和三维射影空间p里也可以建立射影坐标系。 在p上取三个不同的点A0，A1和E。若p为p上任意点，令交比：

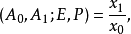
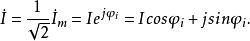
就得到p的射影坐标(x0，x1)。

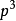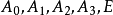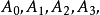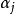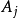在 里，取五点 ，其中每四点不共面。取以 为顶点的四面体， 令 为顶点 的对面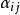， 为棱AjAj的对棱，而 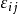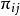， 依次为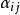 和E，p所确定的平面(i，j=0，1，2，3)。令交比：

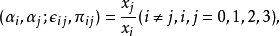
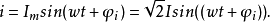
则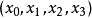 是p点的射影坐标。

解析方法先给出射影平面p的解析定义。取有序非零三数组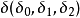 或即三维矢（也称向量）代表p的点，而两个非零矢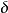，η，若满足关系ξ=λη，其中λ为非零数量，就代表p的同一点。三个线性相关的矢代表p的共线点。

在p中取四点A0，A1，A2，E,它们每三个不共线,并选取代表它们的矢量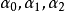, ，使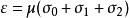 这样，p中每一点p的代表矢ξ都可以写成 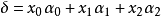的形状，其中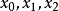不同时为零，而且代表p的任意两个矢都只差一个常数因子。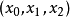就是p点的射影坐标，这个坐标系的基点是 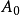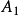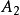， ， ，幺点是E。显然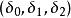本身也是一项射影坐标。扩大欧氏(或仿射) 平面的齐次笛卡儿坐标是扩大平面上的一种特殊射影坐标系。以上两种方法可以互相验证。解析方法以及下面的线性变换法更容易推广到其他类型的基本形。2

线性变换方法射影坐标变换的解析表示是满秩(非异)齐次线性变换。据此,可以得到射影坐标系的又一种建立方式。设在p（或扩大欧氏平面，或扩大仿射平面）上已建立了齐次坐标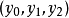 ，令

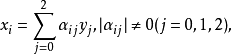
则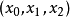 是射影坐标。 这个坐标系的基点和幺点不难从变换方程求得。3

三线坐标这是欧氏平面上非无穷远点的射影坐标的度量解释。设在欧氏平面上取一个三角形的顶点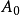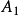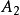，，为射影坐标系的基点。若E为三角形重心（即三条中线的汇合点），则一个非无穷远点p的射影坐标和有向三角形 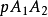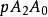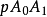， ， 的面积成比例；若E为三角形内心（内接圆心），则p的射影坐标和它到三角形三边 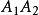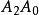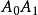， ， 的有向距离成比例。4