例子
内心有三线 1:1:1,这就是说,从三角形 ABC 的内心到边 BC、 CA、AB 的有向距离和实际距离有序三元组 (r, r, r) 成比例,这里 r 是三角形 ABC内切圆的半径。注意到记号 x:y:z 用比例冒号区分三线和实际有向距离。实际距离有序三元组 (kx, ky, kz),能从比例 x : y : z 得到,1
利用面积关系不难算得
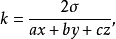
这里 a, b, c 分别是边长 BC、 CA、 AB, σ = ABC 的面积。(“逗号记法”应该避免使用。因为记号 (x, y, z) 意味着是一个有序三元组,不允许 (x, y, z) = (2x, 2y, 2z) 之类运算;然而“比号记法”允许 x : y : z = 2x : 2y : 2z。)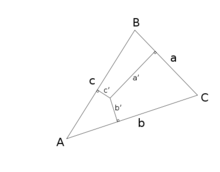
设 A、B 和 C 不仅表示三角形的顶点,也是在相应顶点的角。一些熟知点的三线如下:
A = 1 : 0 : 0
B = 0 : 1 : 0
C = 0 : 0 : 1
内心 = 1 : 1 : 1
A-旁心 = −1 : 1 : 1
B-旁心 = 1 : −1 : 1
C-旁心 = 1 : 1 : −1
外心 = cos A : cos B : cos C
垂心 = sec A : sec B : sec C
九点圆圆心 = cos(B − C) : cos(C − A) : cos(A − B)
重心 = bc : ca : ab = 1/a : 1/b : 1/c = csc A : csc B : csc C
类似重心 = a : b : c = sin A : sin B : sin C
注意到,内心一般不是重心,重心有重心坐标 1:1:1(它们和实际有向面积 BGC、 CGA、AGB 成比例,这里 G = 重心)。
公式利用三线坐标可将许多代数方法运用于三角形几何。比如,三点1
P = p : q : r
U = u : v : w
X = x : y : z
是共线的,当且仅当行列式等于 0。这性质的对偶是三条直线
pα + qβ + rγ = 0
uα + vβ + wγ = 0
xα + yβ + zγ = 0
交于一点(若无穷远点,即平行)当且仅当 D = 0。
另外可算得三角形 PUX 的面积= KD,这里 K = abc/8σ,如果 PUX 和 ABC定向相同,定向相反则 K = - abc/8σ。
许多三次曲线用三线容易表示。比如,中枢自等共轭三次曲线 Z(U,P),作为点 X 的轨迹使得 X 的 P-等共轭点位于直线 UX上,由行列式方程确定。
一些有名的三次曲线 Z(U,P):
Thomson 三次曲线: Z(X(2),X(1)), 这里 X(2) =重心, X(1) =内心
Feuerbach 三次曲线:Z(X(5),X(1)),这里 X(5) =费尔巴哈点
Darboux 三次曲线: Z(X(20),X(1)),这里 X(20) =De Longchamps 点(De Longchamps point)
Neuberg 三次曲线: Z(X(30),X(1)),这里 X(30) =欧拉无穷远点
坐标变换一点具有三线α:β:γ,则重心坐标为aα:bβ:cγ,这里a,b,c是三角形三条边长。相反地,重心坐标为α:β:γ的点有三线α/a:β/b:γ/c。
三线坐标和2维笛卡尔坐标之间存在转换公式。给定一个参考三角形ABC,将顶点B的位置表示成一个笛卡尔坐标的有序组,将其代数地写成一个以顶点C为起点的向量a。类似地定义顶点A为b。然后任何点P关于参考三角形ABC能定义一个2维笛卡尔坐标系,写成向量p= αa+ βb。如果点P有三线坐标x:y:z,那么变换公式是:
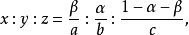
反过来,
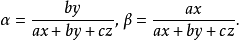




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国