[科普中国]-孤立奇点

定义

若 在 不解析，但在 的某一去心邻域 内解析，则称 是 的孤立奇点。

奇点分为孤立奇点和非孤立奇点。

设为的孤立奇点，在的去心邻域内，的洛朗级数为：

根据展开式的不同情况将孤立奇点分为：

（1）可去奇点

（2）(m级)极点

（3）本性奇点1

可去奇点设为的孤立奇点，在的去心邻域内，的洛朗级数为：

若无负幂项，，则为的可去奇点。

例如，函数在处不解析，它的洛朗展开式为：

展开式中并不含负幂项，那么 称为可去奇点。1

极点设为的孤立奇点，在的去心邻域内，的洛朗级数为：

若的负幂项只有m项，即

，其中，

由于在的去心邻域内解析，故，则为的(m极)极点

例如， ， 是它的一个3级极点。1

本性奇点设为的孤立奇点，在的去心邻域内，的洛朗级数为：

若的负幂项有无穷多项，不存在，也不是，则称为的本性奇点。

例如，函数， 是的本性奇点。1

分类判别规则设为的孤立奇点，根据 时的极限分类：1

（1）可去奇点 存在且有界

（2）极点

（3）本性奇点不存在，且不为

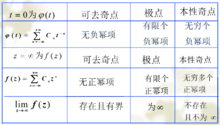
无穷远处设函数 在无穷远点 的去心邻域 内解析，其洛朗级数为：，令 ，则在 的去心邻域 内解析，的洛朗级数为，则如下图1