简介
在数学中,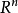 中的非空闭合凸集A的支撑函数
中的非空闭合凸集A的支撑函数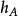 描述了支撑原始集A的超平面的距离。 支撑函数是
描述了支撑原始集A的超平面的距离。 支撑函数是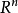 上的凸函数。 任何非空的封闭凸集A由
上的凸函数。 任何非空的封闭凸集A由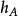 唯一确定。 此外,作为集合A的函数的支撑函数与许多几何操作相兼容,例如缩放,平移,旋转和闵可夫斯基加法。 由于这些属性,支撑函数是凸几何中最重要的基本概念之一。1
唯一确定。 此外,作为集合A的函数的支撑函数与许多几何操作相兼容,例如缩放,平移,旋转和闵可夫斯基加法。 由于这些属性,支撑函数是凸几何中最重要的基本概念之一。1
定义支撑函数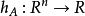 中的非空封闭凸集A由下式确定:
中的非空封闭凸集A由下式确定:
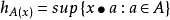
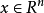 。当x是单位向量时,它的解释是最直观的:根据定义,A包含在封闭的半空间
。当x是单位向量时,它的解释是最直观的:根据定义,A包含在封闭的半空间
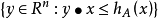
并且在这个半空间的边界中至少有一个A点

因此,超平面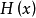 称为具有外部(或外部)单位法向量x的支撑超平面。 外部这个词在这里很重要,因为x的方向起作用,所以集合
称为具有外部(或外部)单位法向量x的支撑超平面。 外部这个词在这里很重要,因为x的方向起作用,所以集合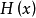 通常不同于
通常不同于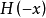 。 现在
。 现在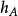 是
是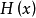 与原点的(有符号)距离。2
与原点的(有符号)距离。2
举例A = {a}的支撑函数是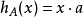 。
。
欧几里得单位球B1的支撑函数是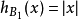 。
。
如果A是具有端点-a的原点的线段,则A是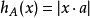 。
。
属性作为x的函数紧凑凸集的支撑函数是实值和连续的,但是如果集合是无界的,则其支撑函数被扩展为实值(它的值为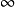 )。 由于任何非空闭合凸集是其支撑半空间的交集,所以函数
)。 由于任何非空闭合凸集是其支撑半空间的交集,所以函数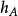 唯一地确定A。 这可以用于分析描述凸集的某些几何属性。 例如,如果且仅
唯一地确定A。 这可以用于分析描述凸集的某些几何属性。 例如,如果且仅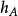 是偶函数,则集合A相对于原点是点对称的。
是偶函数,则集合A相对于原点是点对称的。
一般来说,支持功能是不可区分的。 然而,定向导数存在并产生支持集的支持功能。 如果A是紧凑且凸的,并且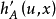 表示方向x上u≠0的
表示方向x上u≠0的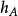 的方向导数,我们有
的方向导数,我们有
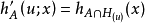
这里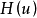 是上面定义的具有外部法向量u的A的支撑超平面。 如果
是上面定义的具有外部法向量u的A的支撑超平面。 如果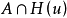 是单例
是单例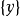 ,则说明支撑函数在u处是可微分的,其梯度与y重合。 相反,如果
,则说明支撑函数在u处是可微分的,其梯度与y重合。 相反,如果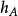 在u是可微分的,则
在u是可微分的,则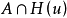 是单例的。 因此,当且仅当A严格为凸(A的边界不包含任何线段)时,
是单例的。 因此,当且仅当A严格为凸(A的边界不包含任何线段)时,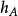 在所有点u≠0时是可微分的。
在所有点u≠0时是可微分的。
它的定义直接遵循支持函数是正同质的:
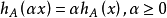
和
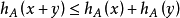
因此,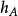 是凸函数。 在凸几何中,这些属性表征支撑函数是至关重要的:
是凸函数。 在凸几何中,这些属性表征支撑函数是至关重要的: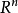 上的任何正齐次、凸实值函数是非空紧凑凸集。 已知有几个证明,一个正在使用的事实是,正均匀、凸实值函数的勒让德变换是紧凑凸集的(凸)指标函数。
上的任何正齐次、凸实值函数是非空紧凑凸集。 已知有几个证明,一个正在使用的事实是,正均匀、凸实值函数的勒让德变换是紧凑凸集的(凸)指标函数。
许多作者将支撑函数限制在欧几里德单位球体上,并将其视为Sn-1的函数。 均匀性属性表明,这个限制确定了如上定义的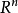 上的支撑函数。3
上的支撑函数。3
作为A的函数扩展集合的支持函数与原始集合A密切相关:
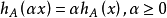
和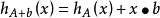
后者概括为
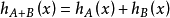
其中A + B表示闵可夫斯基总和:
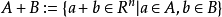
两个非空紧凑凸集A和B的豪斯多夫距离 可以用支持函数来表示,
可以用支持函数来表示,
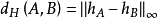
作为集合A的函数的支撑函数的属性有时被总结为说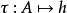 将非空紧凑凸集的集合映射到 在正均匀延伸为凸的球体上的所有实值连续函数的锥。 稍微滥用术语,
将非空紧凑凸集的集合映射到 在正均匀延伸为凸的球体上的所有实值连续函数的锥。 稍微滥用术语, 有时被称为线性,因为它尊重闵可夫斯基加法,尽管它不是在线性空间上定义的,而是在非空紧凑凸集的(抽象)凸锥上。 映射
有时被称为线性,因为它尊重闵可夫斯基加法,尽管它不是在线性空间上定义的,而是在非空紧凑凸集的(抽象)凸锥上。 映射 是具有豪斯多夫度量的锥体之间的等距,并且具有均匀范数的Sn-1上的连续函数族的子像素。4
是具有豪斯多夫度量的锥体之间的等距,并且具有均匀范数的Sn-1上的连续函数族的子像素。4




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国