[科普中国]-杨辉三角

简介

杨辉三角，是二项式系数在三角形中的一种几何排列。在欧洲，这个表叫做帕斯卡三角形。帕斯卡（1623----1662）是在1654年发现这一规律的，比杨辉要迟393年，比贾宪迟600年。杨辉三角是中国古代数学的杰出研究成果之一，它把二项式系数图形化，把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的优美结合1。

概述前提：每行端点与结尾的数为1.

每个数等于它上方两数之和。

每行数字左右对称，由1开始逐渐变大。

第n行的数字有n项。

第n行数字和为2n-1。

第n行的m个数可表示为 C(n-1，m-1)，即为从n-1个不同元素中取m-1个元素的组合数。

第n行的第m个数和第n-m+1个数相等 ，为组合数性质之一。

每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和，这也是组合数的性质之一。即 C(n+1,i)=C(n,i)+C(n,i-1)。

(a+b)n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。

将第2n+1行第1个数，跟第2n+2行第3个数、第2n+3行第5个数……连成一线，这些数的和是第4n+1个斐波那契数；将第2n行第2个数(n>1)，跟第2n-1行第4个数、第2n-2行第6个数……这些数之和是第4n-2个斐波那契数。

将各行数字相排列，可得11的n-1（n为行数）次方：1=11^0; 11=11^1; 121=11^2……当n>5时会不符合这一条性质，此时应把第n行的最右面的数字"1"放在个位，然后把左面的一个数字的个位对齐到十位... ...，以此类推，把空位用“0”补齐，然后把所有的数加起来，得到的数正好是11的n-1次方。以n=11为例，第十一行的数为：1,10,45,120,210,252,210,120,45,10,1，结果为 25937424601=1110。

应用性质5和性质7是杨辉三角的基本性质，是研究杨辉三角其他规律的基础。

与杨辉三角联系最紧密的是二项式乘方展开式的系数规律，即二项式定理。例如在杨辉三角中，第3行的三个数恰好对应着两数和的平方的展开式的每一项的系数（性质 8），第4行的四个数恰好依次对应两数和的立方的展开式的每一项的系数，即 ，以此类推。

又因为性质5：第n行的m个数可表示为C(n-1,m-1)，即为从n-1个不同元素中取m-1个元素的组合数。因此可得出二项式定理的公式为：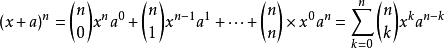

因此，二项式定理与杨辉三角形是一对天然的数形趣遇，它把数形结合带进了计算数学。求二项式展开式系数的问题，实际上是一种组合数的计算问题。用系数通项公式来计算，称为“式算”；用杨辉三角形来计算，称作“图算”2。

数在杨辉三角中的出现次数由1开始，正整数在杨辉三角形出现的次数为∞,1, 2, 2, 2, 3, 2, 2, 2, 4, 2, 2, 2, 2, 4, ... （OEIS:A003016）。最小而又大于1的数在贾宪三角形至少出现n次的数为2, 3, 6, 10, 120, 120, 3003, 3003, ... （OEIS:A062527）

除了1之外，所有正整数都出现有限次，只有2出现刚好一次，6,20,70等出现三次；出现两次和四次的数很多，还未能找到出现刚好五次的数。120,210,1540等出现刚好六次。（OEIS:A098565）

因为丢番图方程 有无穷个解，所以出现至少六次的数有无穷个多。解为 ，其中Fn表示第n个斐波那契数（F1=F2=1）。

3003是第一个出现八次的数。

历史沿革北宋人贾宪约1050年首先使用“贾宪三角”进行高次开方运算。

杨辉，字谦光，南宋时期杭州人。在他1261年所著的《详解九章算法》一书中，辑录了如上所示的三角形数表，称之为“开方作法本源”图，并说明此表引自11世纪中叶（约公元1050年）贾宪的《释锁算术》，并绘画了“古法七乘方图”。故此，杨辉三角又被称为“贾宪三角”。

元朝数学家朱世杰在《四元玉鉴》（1303年）扩充了“贾宪三角”成“古法七乘方图”。

意大利人称之为“塔塔利亚三角形”（Triangolo di Tartaglia）以纪念在16世纪发现一元三次方程解的塔塔利亚。

在欧洲直到1623年以后，法国数学家帕斯卡在13岁时发现了“帕斯卡三角”。

布莱士·帕斯卡的著作Traité du triangle arithmétique（1655年）介绍了这个三角形。帕斯卡搜集了几个关于它的结果，并以此解决一些概率论上的问题，影响面广泛，Pierre Raymond de Montmort（1708年）和亚伯拉罕·棣·美弗（1730年）都用帕斯卡来称呼这个三角形。

21世纪以来国外也逐渐承认这项成果属于中国，所以有些书上称这是“中国三角形”（Chinese triangle）

历史上曾经独立绘制过这种图表的数学家有：

贾宪 中国北宋 11世纪 《释锁算术》

杨辉 中国南宋1261《详解九章算法》记载之功

朱世杰 中国元代 1299《四元玉鉴》级数求和公式

阿尔·卡西 阿拉伯 1427《算术的钥匙》

阿皮亚纳斯 德国 1527

米歇尔.斯蒂费尔 德国 1544《综合算术》二项式展开式系数

薛贝尔 法国 1545

B·帕斯卡 法国 1654《论算术三角形》

其实，中国古代数学家在数学的许多重要领域中处于遥遥领先的地位。中国古代数学史曾经有自己光辉灿烂的篇章，而杨辉三角的发现就是十分精彩的一页。

在编程中实现杨辉三角在编程实现中较为容易。最常见的算法便是用上一行递推计算；也有运用和组合的对应关系而使用阶乘计算的，然而后者速度较慢且阶乘容易溢出。编程的输出大多相类，此处并不过多添加截图。

C、C++、C#、Java 语言之间的语法也大多相类，因此这里也不会将每一种算法都在这些语言中各实现一遍。要在这些语言的版本间修改，实际上只需注意一些简单的语法和函数名称的改变，如 C 的 int yh[M][M] 应改写为 Java 的 int[][] yh = new int[M][M]、C# 的 int[,] yh=new int[M,M]；C printf 应使用 Java 的 System.out.print、C# 的 Console.Write 、C++ 中更智能的 cout 来替换。

C++#include#includeusing namespace std;int main(){ const int n = 15; const int m = 2 * n-1; int arr[n + 1][m] = { 0 }; for (int i = 0; i Python较为便捷，代码量较少的实现方式如下：

# -*- coding: utf-8 -*-#!/usr/bin/env pythondef triangles(): L = [1] while True: yield L L.append(0) L = [L[i - 1] + L[i] for i in range(len(L))]该方式用到了列表生成式，理解起来较困难，下面是另一种方式：

def triangles(): ret = [1] while True: yield ret for i in range(1, len(ret)): ret[i] = pre[i] + pre[i - 1] ret.append(1) pre = ret[:]另一个不用生成器的版本：

def YangHui (num = 10): LL = [[1]] for i in range(1,num): LL.append([(0 if j== 0 else LL[i-1][j-1])+ (0 if j ==len(LL[i-1]) else LL[i-1][j]) for j in range(i+1)]) return LL