定理介绍
三角形外角平分线定理:三角形外角的平分线如果和对边的延长线相交,它按照夹相应角的两边的比外分对边。如下图,在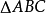 中,外角
中,外角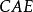 的平分线
的平分线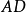 交
交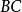 的延长线于
的延长线于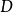 ,则
,则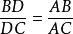 。1
。1
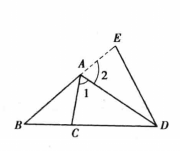
定理的证明证法一如图1,在BA的延长线上任取一点E,连接DE2

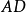 是
是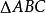 中
中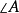 的外角平分线,
的外角平分线,
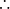
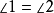 即
即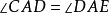 ,
,
 由三角形等角定理得:
由三角形等角定理得:
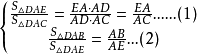
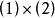 得:
得: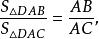
又
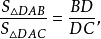
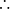
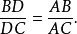
证法二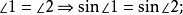
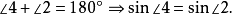
由正弦定理,得:
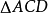 中,
中,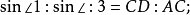
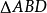 中,
中,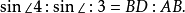
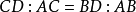 ,
,
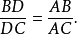
三角形外角平分线逆定理如图1,若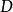 是
是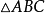 的
的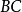 边延长线上的一个点,且满足
边延长线上的一个点,且满足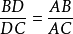 ,则
,则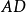 是
是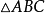 的
的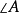 的外角平分线。
的外角平分线。
**证明:**如图1,在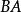 的延长线上任取一点
的延长线上任取一点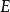 ,连接
,连接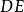 。
。

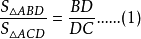
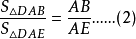
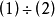 得
得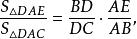

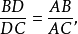
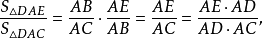
 由三角形等角逆定理得:
由三角形等角逆定理得: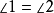 ,即
,即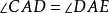 或
或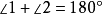 ,即
,即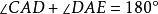 ,
,

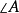 是
是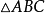 的外角,
的外角,
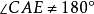 ,即
,即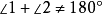 ,也就是
,也就是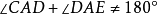 ,
,
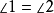 ,即
,即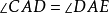 ,
,
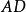 是
是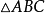 的
的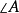 的外角平分线。2
的外角平分线。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国