定义
设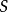 是群
是群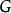 的一个子集,称
的一个子集,称
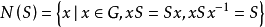 为
为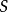 在
在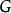 中的正规化子,元素
中的正规化子,元素 的正规化子记为
的正规化子记为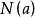 。1
。1
相关定理定理1设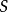 是群
是群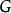 的任一非空子集,则
的任一非空子集,则
(1)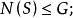
(2) 当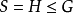 时,
时,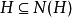 且
且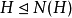 。1
。1
证明(1)因为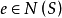 ,故
,故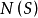 非空,又在
非空,又在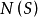 中任取x,y,则
中任取x,y,则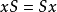 ,
,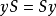 ,从而
,从而
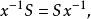
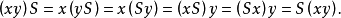 即
即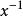 ,
,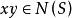 ,故
,故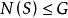 。
。
(2)任取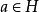 ,由于H是子群,故
,由于H是子群,故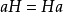 从而
从而
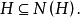 又任取
又任取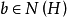 ,则
,则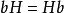 ,从而
,从而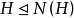 。
。
如果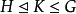 ,则对K中任意元素k便有
,则对K中任意元素k便有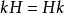 ,从而便有
,从而便有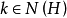 ,即
,即
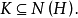 这就是说子群的正规化子
这就是说子群的正规化子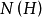 (也叫H的正规化群)是
(也叫H的正规化群)是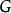 中以H作为其正规子群的最大子群。
中以H作为其正规子群的最大子群。
显然子群H的正规化子是整个群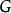 当且仅当H是群
当且仅当H是群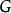 的一个正规子群,另外也可能出现另一种极端,即
的一个正规子群,另外也可能出现另一种极端,即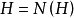 ,例如三次对称群
,例如三次对称群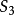 的子群
的子群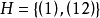 就属于这种情况。
就属于这种情况。
定理2设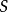 是群
是群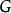 的一个非空子集,
的一个非空子集,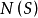 为
为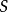 在
在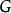 中的正规化子,则
中的正规化子,则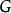 中与共轭的子集数等于
中与共轭的子集数等于
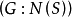 ,即S的所有共轭子集与
,即S的所有共轭子集与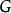 关于
关于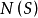 的所有陪集间可建立双射。1
的所有陪集间可建立双射。1
证明 令是中含的共轭子集类(即与共轭的全体子集),再令
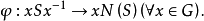 若
若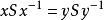 ,则便有
,则便有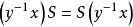 ,从而
,从而
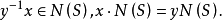 即
即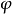 是M到
是M到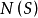 的左陪集的一个映射,又易知
的左陪集的一个映射,又易知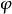 还是满射和单射,从而为双射。
还是满射和单射,从而为双射。
定理3pq阶群(p,q为素数且p




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国