[科普中国]-图解法

图解法解线性规划问题：只含有两个决策变量的线性规划问题，可以通过在平面上作图的方法求解，这种求解线性规划问题的方法称为图解法。该方法简单直观，有助于我们理解求解线性规划问题的基本原理，用图解法解题时，不必将数学模型标准化，易于施行，但是我们一般只用图解法求解含两个变量的线性规划问题。3

图解法解其他数学运算：图解法是指利用图形来解决数学运算的方法。数学运算的本质是通过寻找数与数之间的关系来解决实际问题，整个过程比较抽象。如果我们能够利用图形这种工具，将复杂的数字之间的关系用图形形象地表示出来，能够更快更准地解决问题。

当我们用图解法解线性规划问题时，遵从如下步骤：

第一步，在平面上建立平面直角坐标系；

第二步．图示约束条件，找出可行域或判定可行域是空集；

第三步，图示目标函数，寻找最优解。1

例1 试用图解法求解下面的线性规划问题：

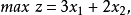
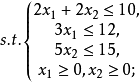
解 首先，按如下步骤绘出可行域（图1中阴影部分）：

(1)绘出平面直角坐标系；

(2)绘出直线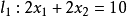，第一个约束不等式是“≤”，故可行域位于直线的左下方；

(3)同理，依次绘出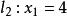直线 与直线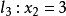 ，判别可行域的方位；

(4)根据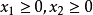 ，绘出可行域；

其次，目标函数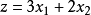 可以变形为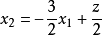 ，即相应的直线族在 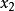轴上截上截距的2倍是目标函数值。

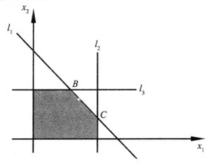
我们可以看到最优值应该在顶点C(4，1)取得，最优值是16。若求目标函数的最小值，则最小值是0，在原点O(0，0)取得。

通过观察可行域，发现：可行域中任意两点连线上的点仍在可行域内，即可行域是凸集，在描绘可行域时，我们亦可以利用原点判别可行域与已知直线的关系。3

1．有唯一最优解的情况

例1即为此情形。

2．有多个最优解的情况

若将例1中的目标函数变更为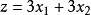 ，则目标函数族与线段BC所在的直线平行，线段BC上的所有点均是最优解，最优值唯一。

3．无有限最优解的情况

若某个线性规划问题的可行域是无界的，则有可能出现无有限最优解的情况，如将例1变更为：

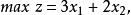
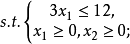
其可行域是可以向上无限延伸的无界区域，最优解是 。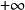

同时需注意到可行域无界并不意味着一定无有限最优解，若将本例中目标函数的最大值变更为求目标函数的最小值，此时有有限最优值0。

一般的，若对某实际问题进行求解时，出现了无有限最优解的情况，多表示数学模型中缺少必要的约束条件。

4．可行域是空集

若某个线性规划问题的约束条件是

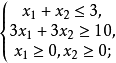则此问题的可行域是空集，该问题无可行解。

若解某个实际问题的数学模型时，出现可行域是空集的情形，多是某一约束条件出现了偏差。

前面我们已经研究了图解法的基本理论，在现实操作中，由于种种原因可能会引起偏差乃至错误。

如果约束不等式的右端项的数值较大，远大于工艺系数，我们用图解法解决相应问题时就可能由于观测或操作的原因（画图或直线平移等）导致错误发生；所得到的最优解并非是真正的最优解，为此，我们可以根据定理（如果线性规划问题（P）有有限最优解，则其目标函数的最优值一定可以在可行域的顶点上达到），采用顶点比较法寻求线性规划问题的最优解，所谓顶点比较法是先求出可行域的所有顶点的坐标，而后分别计算目标函数在顶点的函数值，通过比较大小而得出最优值的方法。

除顶点比较法外，还可以用斜率比较法减少上述错误的发生，所谓斜率比较法是指先求出目标函数的斜率（称为目标斜率），而后，将难以判别是否是最优解的顶点的边界连线所在直线的斜率求出，将其与目标函数进行比较，最终得出最优解的方法。

此外，还可以利用目标函数参与法求简单线性规划的最优整数解。3

一般说来，图解法适用于绝大部分题型，尤其是在行程问题、年龄问题、容斥问题等强调分析过程的题型中运用得很广。图解法简单直观，能够清楚表现出问题的过程变化，但是容易出错，在画图形的时候一定要保证图形和数字保持一一对应的关系。2

某人上午8点要去上班，可是发现家里的闹钟停在了6点10分，他上足发条但忘了对表就急急忙忙地上班去了，到公司一看还提前了10分钟。中午12点下班后，回到家一看，闹钟才11点整，假定此人上班、下班在路上用的时间相同，那么他家的闹钟停了多少分钟？

A.100 B.90 C.80 D.70

解析：这个忘了上发条的时钟问题实际对应的是一个时间轴，我们选择此模型分析题干情境。

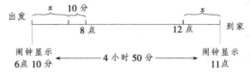
如图，这个人8点上班，12点下班，把相应的信息对应在时间轴上。到公司时提前了10分钟说明实际抵达时间为7点50分。上下班时间相同，设为x分钟。把这人出发与回到家的时间也分别写在对应的时间轴上。

闹钟从6点10分走到11点，共走了4小时50分，也就相当于2x+10分钟+4小时，即4小时50分=2x+10分钟+4小时，可知x=20分钟。

从而可知这个人从家出发的时间为7点30分，而此时闹钟停在了6点10分，所以闹钟停了60+20=80分钟。2