[科普中国]-第一类误差

假设检验1：事先对总体参数或分布形式作出某种假设，然后利用样本信息来判断原假设是否成立的过程。

假设检验的类型:统计假设一般可分为参数假设与非参数假设。参数假设是指总体分布类型已知，对未知参数的统计假设。检验参数假设问题成为参数检验。当总体分布类型为正态分布时，则为正态总体参数检验。非参数假设是指总体分布类型不明确，对参数的各种统计假设。检验非参数假设问题称为非参数检验，也称分布检验。

假设检验的特点:1、统计检验的假设是关于总体特征的假设；2、用于检验的方法是以检验统计量的抽样分布为理论根据的；3、作出的结论是概率性的，不是绝对的肯定或绝对的否定。

假设检验是根据样本的信息，利用小概率原理来对总体进行推断。但是，小概率事件在一次试验中毕竟可能发生，因此假设检验难免要犯两类错误。两个假设分别为原假设(虚无假设)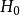： ，备择假设：。

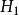第一类错误（Ⅰ类错误）也称为 α错误，是指当虚无假设(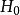 )正确时，而拒绝 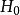所犯的错误。发生的概率为α。这意味着研究者的结论并不正确，即观察到了实际上并不存在的处理效应。

第二类错误（Ⅱ类错误）也称为β错误，是指虚无假设错误时，反而接受虚无假设的情况。发生的概率为β。即没有观察到存在的处理效应。

检验统计量是随机变量， 有一定的波动性，在进行假设检验时，即使原假设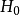为真，而由样本实验数据计算的统计量值仍有一定的概率α落入拒绝域内，从而错误地拒绝原假设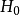。α为犯第一类错误的概率，称为显著性水平。1－α为当原假设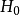为真而作出正确判断的概率。α越小，犯第一类错误的概率就越小。第一类错误可能产生原因2：1、样本中极端数值。2、采用决策标准较宽松。

犯Ⅰ类错误的影响较大，由于报告了本来不存在的现象，则因此现象而衍生出的后续研究、应用的危害将是不可估量的。相对而言，Ⅱ类错误的危害则相对较小，因为研究者如果对自己的假设很有信心，可能会重新设计实验，再次来过，直到得到自己满意的结果（但是如果对本就错误的观点坚持的话，可能会演变成Ⅰ类错误）。

1、 α+β不一定等于1。

2、在样本容量确定的情况下，α与β不能同时增加或减少，而是此消彼长的关系1。

在实际应用中，若水平α很小，原假设 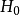不会轻易被否定． 如果样本落入了否定域，作出“否定原假设 H0”的结论就比较可靠，此时犯第一类错误的概率很小。 反之，当 α 很小时，如果样本落入了接受域，作出“接受原假设 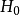”的结论就未必可靠，这只能表明: 在所选定的水平下没有充分根据否定原假设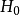，但绝不意味着有充分的根据说明它正确，因为此时犯第二类错误的概率可能很大。而在求解两类错误概率大小的关键是明白接受域和拒绝域的具体内容，按条件概率的定义来求解。 而为了控制犯两类错误的概率，通常有两种方法1: ①适当地增大样本个数 n，理论上可行，在实际操作中不太可行。 ②限制犯第一类错误概率的原则，当样本个数 n 确定后，在保证犯第一类错误的概率不超过指定数值α( 0