[科普中国]-熵率

基本介绍定义

如果给定一个长度为n的随机变量序列，我们自然会问：该序列的熵随n如何增长?下面定义这个增长率，我们称为熵率。

当如下极限存在时，随机过程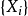 的熵率定义为2

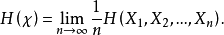
举例说明下面考虑几个简单的随机过程例子及其相应的熵率。2

1．打字机。假定一台打字机可输出m个等可能的字母。由此打字机可产生长度为n的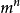个序列，并且都等可能出现。因此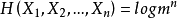， ，熵率为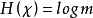 比特/字符。随机过程的熵率43符。

2．i.i.d. 随机变量序列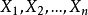 。此时，有

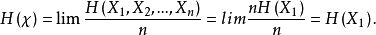这正是我们所期望的每字符的熵率。

3．独立但非同分布的随机变量序列。在此情形下，有

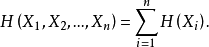
但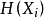 不全相等。我们可以选择 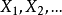的一个分布序列，使 的极限不存在。例如取二值随机分布序列，其中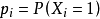 不是常数，而为i的函数。通过细心选取 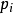匕纠可使得式 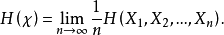的极限不存在。例如，对 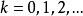取

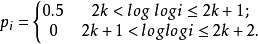
此时，该序列的情况是，满足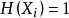 的随机变量序列(可以任意长)之后，紧接着是更长以指数变化的序列满足 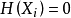。所以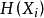， 的累积平均值将在0与1之间振荡，从而不存在极限。因此，该过程的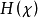无定义。

我们也可以定义熵率的一个相关的量(如果下列极限存在)：

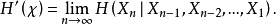
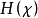和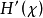这两个量反映了熵率概念的两个不同方面。第一个量指的是n个随机变量的每字符熵，而第二个量指在已知前面n-1随机变量的情况下最后一个随机变量的条件熵。2

重要定理定理1对于平稳随机过程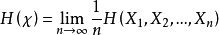，式和式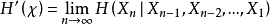中的极限均存在且相等：2

=

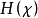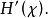
我们先来证明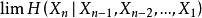存在。

定理2对于平稳随机过程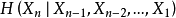，随n递减且存在极限。

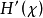证明：

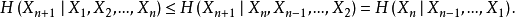
其中的不等式由条件作用使熵减小这个性质得到，而等式由该过程的平稳性得到。由于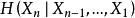是非负且递减的数列，故其极限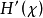存在。

接下来使用数学分析中的一个如下简单结论。2

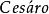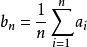定理3均值：若，且，则。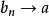

证明：(非正式思路)由于序列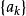中的大部分项最终趋于a，那么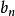，是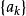的前n项的平均，也将最终趋于a。正式证明阅参考资料。2

定理1的证明 由链式法则

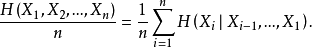
也就是说，熵率为条件熵的时间平均。然而，我们已经知道条件熵趋于极限H'，因此，由定理3可知，条件熵的累积平均存在极限，且此极限就是其通项的极限H'。于是，由定理2，

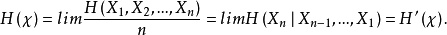
研究随机过程熵率的重要意义体现在平稳遍历过程的AEP。2

对任何平稳过程，熵率均有恰当的定义。而对于马尔可夫链，计算熵率尤为容易。

马尔可夫链对于平稳的马尔可夫链，熵率为

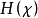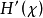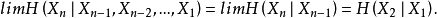==其中的条件熵可根据给出的平稳分布计算得到。注意到，平稳分布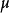为下列方程组的解：

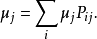
其中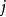为任意值。2

定理4设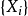为平稳马尔可夫链，其平稳分布为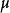，转移矩阵为P。则熵率为

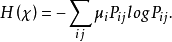
证明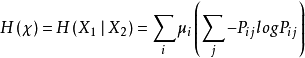：。2