[科普中国]-积和式

定义

为了给定n阶积和式的定义，我们来定义一下几个名称：

线性函数设f是F^n上的一个k元函数。如果对每一个i，1≤i≤k，均有

f(ξ1,...,ξ(i-1),λη+μζ,ξ(i+1),...,ξk)=λf(ξ1,...,ξ(i-1),η,ξ(i+1),...,ξk)+μf(ξ1,...,ξ(i-1),ζ,ξ(i+1),...,ξk)

其中λ，μ∈F，η，ζ∈F^n，则f称为k重线性函数。

规范设f(ξ1,ξ2,...,ξn)是F^n上的n元函数，且设εi为第i个分量为1，其他分量为0的向量，i=1,2，...,n。如果f(ε1,ε2,...,εn)=1，则称f(ξ1,ξ2,...,ξn)是规范的。

对称设f(ξ1,ξ2,...,ξn)是F^n上的n元函数，如果对于任意整数i，j，1≤i,j≤n，均有

f(ξ1,...,ξi,...,ξj,...,ξk)=f(ξ1,...,ξj,...,ξi,...,ξk)

则称f(ξ1,ξ2,...,ξn)是对称的。

于是我们得到了n阶积和式的定义：

积和式定义给定一个数域F，则称数域Fn上的规范对称n重线性函数叫做n阶积和式(permanent)。2

这和n阶行列式对比：

给定一个数域F，则称数域Fn上的规范反对称n重线性函数叫做n阶行列式(determinant)。

性质对于一个方阵A，A=(aij)，n阶积和式记为perA或者permA2

不难证明，

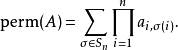
特殊情况，当n=2时，perA=a11a22+a21a12，与行列式只差个符号。因此，积和式有些性质可以类比于行列式。

组合上的解释积和式的定义可以从如下两方面理解，即计算二分图上完美匹配的个数，以及计算一个图上的圈覆盖的权重。

二分图二分图上的完美匹配是算法理论和计算复杂性理论中的重要问题。对于一个n×n的二分图G=(L, R, E)，其中L={1, 2,..., n}是左边结点的集合，R={1', 2', ..., n'}是右边结点的集合，E为边的集合，G的一个完美匹配是{1, 2, ..., n}到{1', 2', ..., n'}的一个双射f，使得(1, f(1)), (2, f(2)), ..., (n, f(n))都在E中出现。

对G，我们可以建立如下n×n的0-1矩阵Ag=(aij)，i,j∈{1,2,...,n}，其中aij=1当且仅当(i,j')属于E。不难验证，perAg的值即是G中完美匹配的个数。这样，我们将积和式的值与二分图完美匹配的个数建立了联系。

图的圈覆盖对于一个图G=(V,E)，V={1, 2, ..., n}为结点集，E为边集。一个G的圈覆盖是一组G中的不相交的圈的集合，且这些圈覆盖所有的点集。由于一个置换可以做环状分解，可以看出一个置换与一个可能的圈覆盖是一一对应的。特别的，G的邻接矩阵的积和式即是G中圈覆盖的数目。

计算复杂性积和式的计算是#P完全的。相对的，行列式可以用高斯消元法等算法在多项式时间内解决。