[科普中国]-测度

定义

定义1：构造一个集函数，它能赋予实数集簇М中的每一个集合E一个非负扩充实数mE。我们将此集函数称为E的测度2。

定义2：设Γ是集合X上一σ代数，ρ ：Γ →R∪{ +∽ }是一集合函数，且ρ满足：

（1）（非负性）对任意的A∈Γ，有ρ(A)≧0;

（2）（规范性）ρ(Φ) = 0；

（3）（完全可加性） 对任意的一列两两不交集合A1，A2，……，An，……有ρ(∪n An)=∑n ρ（An）

则称ρ是定义在X上的一个测度，Γ中的集合是可测集，不在Γ中的集合是不可测集。特别的，若ρ(X) = 1 ，则称ρ为概率测度。

性质

下面的一些性质可从测度的定义导出：3

单调性

测度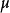 的单调性： 若 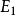和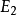 为可测集，而且 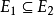，则 。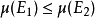

可数个可测集的并集的测度

若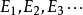 为可测集（不必是两两不交的），则集合 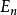的并集是可测的，且有如下不等式（“次可列可加性”）：

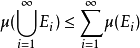
如果还满足并且对于所有的 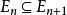， ，则如下极限式成立：

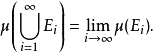
可数个可测集的交集的测度

若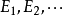 为可测集，并且对于所有的 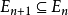， ，则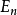 的交集是可测的。进一步说，如果至少一个 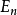的测度有限，则有极限：

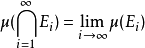
如若不假设至少一个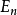 的测度有限，则上述性质一般不成立。例如对于每一个 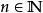，令

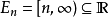
这里，全部集合都具有无限测度，但它们的交集是空集。

完备性

一个可测集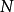称为零测集，如果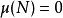。零测集的子集称为可去集，它未必是可测的，但零测集自然是可去集。如果所有的可去集都可测，则称该测度为完备测度。

一个测度可以按如下的方式延拓为完备测度：考虑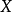的所有这样的子集 F，它与某个可测集 E仅差一个可去集，也就是说 E与 F的对称差包含于一个零测集中。由这些子集 F生成的σ代数，并定义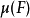的值就等于。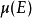

例子

下列是一些测度的例子（顺序与重要性无关）。2

计数测度定义为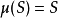 的“元素个数”。

一维勒贝格测度是定义在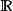 的一个含所有区间的σ代数上的、完备的、平移不变的、满足 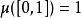的唯一测度。

Circular angle测度是旋转不变的。

局部紧拓扑群上的哈尔测度是勒贝格测度的一种推广，而且也有类似的刻划。

恒零测度定义为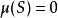 ，对任意的 。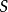

每一个概率空间都有一个测度，它对全空间取值为1（于是其值全部落到单位区间[0,1]中）。这就是所谓概率测度。见概率论公理。

其它例子，包括：狄拉克测度、波莱尔测度、若尔当测度、遍历测度、欧拉测度、高斯测度、贝尔测度、拉东测度。