[科普中国]-满射

定义

一个函数称为满射：如果每个可能的像至少有一个变量映射其上（即像集合B中的每个元素在A中都有一个或一个以上的原像），或者说值域任何元素都有至少有一个变量与之对应。1

满射或盖射（英语：surjection、onto），或称满射函数或映成函数，一个函数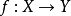 为满射，则对于任意的陪域Y中的元素 y，在函数的定义域X中存在一点 x使得f(x)=y。换句话说， f是满射时，它的值域f(X)与陪域Y相等，或者，等价地，如果每一个陪域中的元素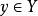 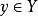其原像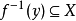 不等于空集合。

例子和反例函数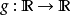 ，定义为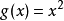 ，不是一个满射，因为，（举例）不存在一个实数满足 。

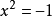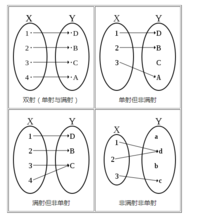
但是，如果把g的陪域限制到只有非负实数，则函数g为满射。这是因为，给定一个任意的非负实数y，我们能对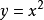 求解，得到 。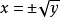

性质（1）函数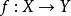为一个满射，当且仅当存在一个函数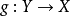满足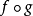等于 Y上的单位函数。（这个陈述等价于选择公理。）

（2）根据定义，函数为双射当且仅当它既是满射也是单射。

（3）如果是满射，则f是满射。

（4）如果f和 g皆为满射，则为满射。

（5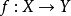）为满射，当且仅当给定任意函数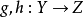满足，则g=h。

（6）如果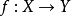为满射，且 B是Y的子集，则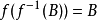，。因此，B能被其原像复原。

（7）任意函数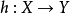都可以分解为一个适当的满射 f和单射g，使得。

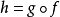（8）如果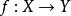为满射函数，则 X在基数意义上至少有跟 Y一样多的元素。

（9）如果 X和Y皆为具有相同元素数的有限集合，则是满射当且仅当 f是单射。