[科普中国]-上界

简介

上界，是与偏序集有关的一个特殊元素。指偏序集中大于或等于它的子集中一切元素的元素。设是偏序集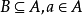， ，若对所有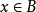 都有xRa，则a称为B在偏序集中的上界，简称B的上界，记为 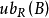。若a是B的上界，对于B的任何上界c，都有 aRc，则a称为B的上确界（或最小上界），记为 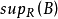。2

实数集R上的定义考虑一个实数集合M。如果有一个实数s，使得M中任何数都不超过s，那么就称s是M的一个上界。

用数学符号表示为：对∀x∈M，都有x≤s，则称s是M的上界（upper bound）。

确界原理：若R的子集M有上界，则必有上确界；若集合M有下界，则必有下确界。

上确界定义：设S是R中的一个数集，若数η∈R满足

（i）对∀x∈S，有η≥x，即η是S的上界；

（ii）对∀aa，即η是S的最小上界（least upper bound），则称η为数集S的上确界；

下确界定义：设S是R的一个数集，若数ξ∈R满足：

（i）对∀x∈S，有ξ≤x，即ξ是S的下界；

（ii）对∀β>ξ,∃x0∈S，使得x0