定义
如果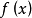 有
有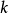 重因式
重因式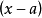 ,即
,即
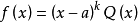 其中,
其中,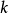 是大于1的自然数,
是大于1的自然数,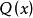 是不含因式
是不含因式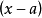 的多项式,则称
的多项式,则称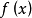 存在重根
存在重根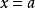 ,且其重数为
,且其重数为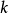 。1
。1
性质根据多项式乘积的导数公式,对函数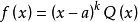 求导可得:
求导可得:
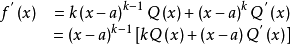 上式中,由于
上式中,由于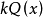 不含因式
不含因式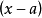 ,而
,而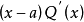 含有因式
含有因式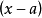 ,于是括号中的
,于是括号中的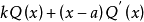 不含有因式
不含有因式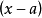 ,因此
,因此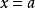 是
是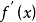 的
的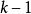 重根。由此可以得到多项式重根有以下性质:
重根。由此可以得到多项式重根有以下性质:
①多项式的重根也是它的导数函数的根,且作为导数根的重数少1。
②当且仅当多项式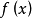 与它的导数
与它的导数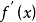 的最高公因式是零次多项式时,多项式
的最高公因式是零次多项式时,多项式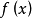 才没有重根。1
才没有重根。1
应用举例判断方程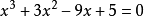 有没有重根。
有没有重根。
解:设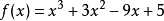 ,则
,则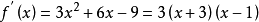 ,即
,即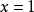 和
和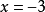 是
是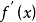 的根,先将这两根分别代入
的根,先将这两根分别代入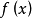 ,由于
,由于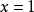 是
是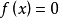 的根,所以
的根,所以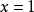 是多项式
是多项式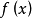 与它的导数
与它的导数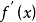 的公根,它就是
的公根,它就是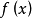 的重根;而
的重根;而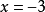 不是
不是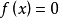 的根。1
的根。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国