定义普通函数
冲激函数的定义为:
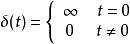
单位冲击函数
通常,单位冲激函数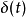 满足:
满足:
(1)当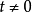 时,
时,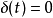
(2)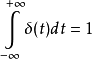
单位冲激函数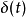 又称Dirac函数或者
又称Dirac函数或者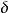 函数。
函数。
注:单位冲激函数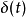 并不是经典意义下的函数,而是一个广义函数(或者奇异函数),它不能用通常意义下的“值的对应关系”来理解和使用,而是通过它的性质来使用。1
并不是经典意义下的函数,而是一个广义函数(或者奇异函数),它不能用通常意义下的“值的对应关系”来理解和使用,而是通过它的性质来使用。1
广义函数
选择一类性能良好的函数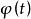 ,称为检验函数
,称为检验函数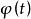 (它相当于定义域),一个广义函数
(它相当于定义域),一个广义函数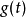 对检验函数空间中的每个函数
对检验函数空间中的每个函数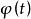 赋予一个数值
赋予一个数值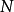 的映射,该数与广义函数
的映射,该数与广义函数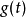 和检验函数
和检验函数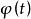 有关,记作
有关,记作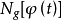 。广义函数可写为
。广义函数可写为
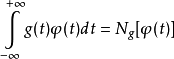
冲击函数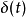 与检验函数的作用效果是从
与检验函数的作用效果是从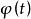 中筛选出它在
中筛选出它在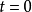 时刻的函数值
时刻的函数值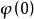 ,这常称为冲击函数的取样性质(或筛选性质)。简言之,能从检验函数
,这常称为冲击函数的取样性质(或筛选性质)。简言之,能从检验函数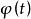 中筛选出函数值
中筛选出函数值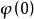 的广义函数就称为冲击函数
的广义函数就称为冲击函数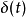 1。
1。
性质筛选性质
如果信号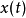 是一个在
是一个在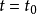 处连续的普通函数,则有
处连续的普通函数,则有
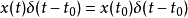
上式表明,信号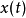 与冲激函数相乘,筛选出连续时间信号
与冲激函数相乘,筛选出连续时间信号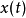 在
在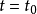 时的函数值
时的函数值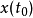 ,可以理解为冲激函数在
,可以理解为冲激函数在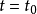 时刻对函数
时刻对函数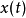 的一瞬间的作用,其值是冲激函数和
的一瞬间的作用,其值是冲激函数和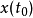 相乘的结果,瞬间趋于无穷大2。
相乘的结果,瞬间趋于无穷大2。
取样性质
如果信号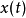 是一个在
是一个在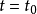 处连续的普通函数,则有
处连续的普通函数,则有
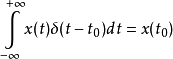
冲激信号的取样特性表明,一个连续时间信号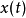 与冲激函数相乘,并在时间域
与冲激函数相乘,并在时间域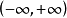 上积分,其结果为信号
上积分,其结果为信号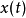 在
在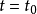 时的函数值
时的函数值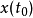 。该式可以理解为冲激函数作用于函数
。该式可以理解为冲激函数作用于函数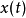 ,趋于稳态时最终作用的结果,即得到信号
,趋于稳态时最终作用的结果,即得到信号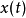 在
在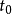 时刻的值
时刻的值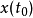 2。
2。
导数性质
冲激函数的导数性质如下:
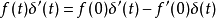 其证明如下:
其证明如下:
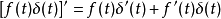
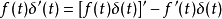
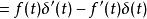
尺度变换
冲激函数的尺度变换性质如下:
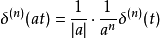
其推论明如下:
(1)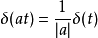
(2)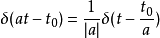
(3) 当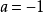 时,
时,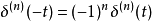
(4)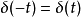 ,
,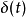 为偶函数
为偶函数
(5)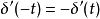 ,
,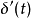 为奇函数
为奇函数
应用
冲激函数可用于信号处理,通过冲激函数来表示复杂的信号,可以简化对复杂信号的一些特性的研究。冲激函数及其延时冲激函数的线性组合来表示或逼近,再利用系统的迭加原理,可以通过简单的信号如单位冲激函数的频谱,以及频域特性来讨论比较复杂信号的频谱。从而减少计算复杂信号频谱的难度11。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国