[科普中国]-一致空间

一致空间

在一致结构和拓扑结构之间的概念区别是在一致空间内可以形式化有关于相对邻近性和点间临近性的特定概念。换句话说，想法如“x邻近于 a胜过 y邻近于 b”在一致空间是有意义的。相对的，在一般拓扑空间内，给定集合 A, B只能有意义的说点 x“任意邻近”A（就是说在 A 的闭包中），或者说 A是比 B更小的 x的“邻域”，但是点间邻近性和相对邻近性不能单独用拓扑结构描述。

一致空间推广了度量空间和拓扑群因此是多数数学分析的根基。2

一致结构一致结构是集合上的一种结构。设X为集合，U为X×X的非空子集族。若U满足下列条件，则称U是X上的一致结构：

1.U的每一个元包含对角线Δ.

2.若U∈U，则U^-1∈U，其中：

U^-1={(x，y)|(y，x)∈U}.

3.若U∈U，则存在V∈U使得V°V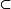U，其中：

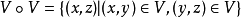4.若U，V∈U，则U∩V∈U.

5.若U∈U并且UVX×X，则V∈U.

具有一致结构U的集合X称为一致空间，记为(X，U)。一致空间的概念是韦伊(Weil，A.)于1938年引入的。布尔巴基(Bourbaki，N.)于1940年首先给予系统的论述。图基(Tukey，J.W.)于1940年用覆盖族定义并研究了一致空间的等价的概念。艾斯贝尔(Isbell，J.R.)于1964年出版的书中，包含了用覆盖叙述的一致空间理论的重要发展.一致空间也可用伪度量族来描述，它是由布尔巴基于1948年给出的。

定义一致空间有三个等价定义。

周围定义

一致空间(X, Φ) 是集合X配备了笛卡尔积X× X的非空子集族（Φ 叫做 X的一致结构或一致性而它的元素叫做周围（法语entourage：邻居或周围））满足如下公理：

如果 U在 Φ 中，则 U包含对角 Δ = { (x, x) : x∈ X}。

如果 U在 Φ 中而 V是包含 U的 X× X的子集，则 V在 Φ 中。

如果 U和 V在 Φ 中，则 U∩ V在 Φ 中。

如果 U在 Φ 中，则存在 V在 Φ 中，使得只要 (x, y) 和 (y, z) 在 V中，则 (x, z) 在 U中。

如果 U在 Φ 中，则 U= { (y, x) : (x, y) ∈U} 也在 Φ 中。

如果省略了最后的性质则称空间为准一致的。注意二三两条是滤子的定义。

通常写 U[x]={y : (x,y)∈U}。在图形上，典型的周围被绘制为围绕“y=x”对角的斑点；U[x] 们则为纵截面。如果 (x,y) ∈ U，则可以说 x和 y是“U-邻近”的。类似的，如果在 X的子集 A中的所有成对的点都是 U-邻近的（就是说如果 A× A被包含在 U中），则 A被称为“U-小”的。周围 U是对称的，如果 (y,x) ∈ U正好在 (x,y) ∈ U的时候。第一个公理声称对于每个周围 U每个点都是 U-邻近于自身。第三个公理保证“同时 U-邻近和 V-邻近二者”也是在一致性中的邻近关系。第四个公理声称对于每个周围 U都有一个周围 V是“一半大”的。最后的公理声称“邻近”关于一致结构的本质对称性质。

一致性 Φ 的基础周围系统是 Φ 的周围的任何集合 B，使得所有 Ф 的周围包含属于 B的一个集合。因此，通常上述性质 2，基础周围系统 B足够无歧义的指定一致 Φ: Φ 是包含 B的一个集合的 X× X的子集的集合。所有一致空间都用由对称周围构成的基础周围系统。

关于一致性的正确直觉可由度量空间的实例提供：如果 (X,d) 是度量空间，集合

这里的

形成了 X的标准一致结构的基础周围系统。则 x和 y是 Ua-邻近的，正好在 x与 y之间距离最多为 a的时候。

一致性 Φ “精细”于在同一个集合上的另一个一致性 Ψ，如果 Φ ⊇ Ψ；此时 Ψ 被称为“粗糙”于 Φ。

伪度量定义

一致空间可以使用伪度量系统来等价的定义，这是对泛函分析（带有半范数提供的伪度量）特别有用的方式。更精确地说，设 f: X× X→ R是在集合 X上的伪度量。逆像 Ua= f（[0,a]）对于 a> 0 可以被证实形成了一致的基础周围系统。由 Ua生成的一致是由单一的伪度量 f所定义的一致。

对于在 X上的伪度量族 (fi)，这个族所定义的一致结构是单独伪度量 fi所定义的一致结构的“最小上界”。这个一致性的基础周围系统由单独伪度量 fi所定义的一直的周围的有限交集的集合来提供。如果伪度量的族是有限的，可以看出同样的一致结构可以定义自单一的伪度量，就是这个族的“上包络” sup fi。

更少琐碎的，可证实允许可数的基础周围系统（并因此特别为由可数的伪度量族定义的一致）可以定义自一个单一伪度量。结论是任何一致结构都可以如上述那样的定义自（可能不可数）伪度量族（参见 Bourbaki：《General Topology》 Chapter IX §1 no. 4）。

一致覆盖定义

一致空间(X,Θ) 是集合 X配备显著的“一致覆盖”族 Θ，它来自 X的覆盖的集合，在按星号精致排序的时候形成了滤子。你可以称呼覆盖 P是覆盖 Q的星号精致(refinement)写为 P