定义
向量的范数是长度概念的推广。设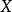 是域
是域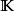 (实数域或复数域)上的线性空间,函数
(实数域或复数域)上的线性空间,函数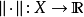 满足条件:
满足条件:
1)对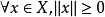 ;且
;且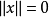 当且仅当
当且仅当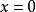 ;
;
2)对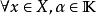 ,有
,有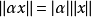 (齐次性);
(齐次性);
3)对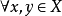 ,有
,有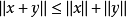 (三角不等式)。
(三角不等式)。
称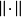 是
是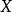 上的一个范数,
上的一个范数,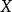 上定义了范数
上定义了范数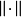 称为**(线性)**赋范空间,记为
称为**(线性)**赋范空间,记为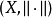 ,有时简记为
,有时简记为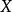 。2
。2
范数诱导的距离在一个赋范空间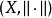 中,通过范数可以自然地定义一个距离,
中,通过范数可以自然地定义一个距离,
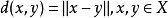 。
。
事实上,由范数公理,对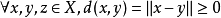 ,且
,且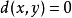 ,当且仅当
,当且仅当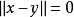 ,即
,即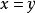 ;
;
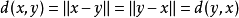 ;
;
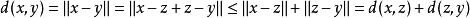 。
。
称赋范空间中这个距离是由范数诱导的距离。1
强(或按范)收敛设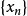 是赋范空间
是赋范空间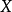 中的点列,
中的点列,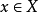 ,如果
,如果
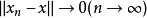 ,
,
称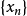 强(或按范)收敛于
强(或按范)收敛于 ,记为
,记为
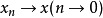 ,
,
或
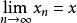 。3
。3
Banach空间如果赋范空间按强收敛是完备的,就称它为Banach空间。4
性质性质1范数是一个连续函数,即当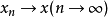 时,
时,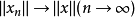 。5
。5
性质2线性运算是连续的,即当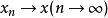 及
及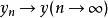 时,
时,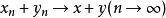 ;
;
当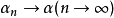 及
及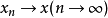 时,
时,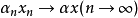 。5
。5
性质3设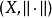 是赋范空间。如果
是赋范空间。如果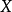 是完备的且级数
是完备的且级数
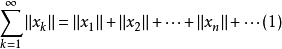
收敛,则级数
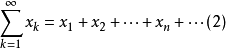
收敛且
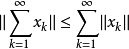 。
。
反之,如果在一个赋范空间中,任意无穷级数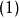 收敛必有级数
收敛必有级数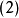 收敛,则空间是Banach空间。6
收敛,则空间是Banach空间。6
拓扑结构如果(V,‖·‖)是规范向量空间,则‖·‖引入度量(距离的概念),并因此导致V上的拓扑。该度量以自然的方式定义:两个向量之间的距离u v由||u-v||给出。这种拓扑正是最弱的拓扑结构,使得“‖”连续,并且与以下意义上的V的线性结构兼容:
向量加法+:V×V→V相对于该拓扑结合是连续的。这直接来自三角不等式。
标量乘法:K×V→V,其中K是V的底层标量场,是联合连续的。这取决于三角不平等和规范的均匀性。
类似地,对于任何半规范向量空间,我们可以将两个向量u和v之间的距离定义为‖u-v‖。这将把这个空间变成一个假的空间(注意这比一个度量要弱),并允许定义诸如连续性和收敛的概念。为了更抽象地说,每个半规范向量空间是一个拓扑向量空间,因此承载了由半规范引起的拓扑结构。
特别感兴趣的是称为Banach空间的完整规范空间。每个规范向量空间V坐在Banach空间内的一个密集子空间;这个Banach空间本质上是由V定义的,称为V的完成。
有限维向量空间上的所有规范从拓扑观点是相等的,因为它们诱导相同的拓扑(尽管所得的度量空间不必相同)。并且,由于任何欧几里德空间是完整的,因此我们可以得出结论,所有有限维的规范向量空间是Banach空间。当且仅当单位球B = {x:‖x‖≤1}紧凑时,规范向量空间V是局部紧凑的,当且仅当V是有限维的情况下才是这种情况;这是雷斯的引理的结果。 (事实上,更一般的结果是真实的:当且仅当它是有限维度时,拓扑向量空间是局部紧凑的,这里的意思是我们不假定拓扑来自一个规范。
信号向量空间的拓扑具有许多不错的属性。给定一个约0的邻域系统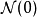 ,我们可以构建所有其他邻域系统:
,我们可以构建所有其他邻域系统:
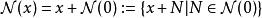
与:
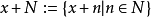
此外,存在由吸收和凸集组成的0的邻域基础。由于该属性在功能分析中非常有用,因此在名称为局部凸空间的情况下研究了具有该属性的规范向量空间的泛化。7




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国