[科普中国]-阶乘

简介

阶乘是基斯顿·卡曼（Christian Kramp，1760～1826）于 1808 年发明的运算符号，是数学术语。

一个正整数的阶乘（factorial）是所有小于及等于该数的正整数的积，并且0的阶乘为1。自然数n的阶乘写作n!。1808年，基斯顿·卡曼引进这个表示法。

计算方法大于等于1任何大于等于1 的自然数n 阶乘表示方法：

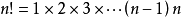
或

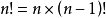
0的阶乘0！=1。

定义的必要性

由于正整数的阶乘是一种连乘运算，而0与任何实数相乘的结果都是0。所以用正整数阶乘的定义是无法推广或推导出0！=1的。即在连乘意义下无法解释“0！=1”。

给“0！”下定义只是为了相关公式的表述及运算更方便。

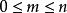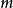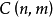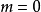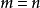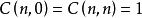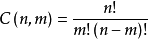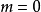在离散数学的组合数定义中，对于正整数 满足条件 的任一非负整数 ， 都是有意义的，特别地在 及 时，有 。 但是对于组合数公式 来说，在 及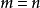 时，都由于遇到0的阶乘没有定义而发生巨大尴尬。

对照结论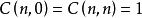 和公式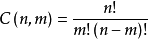 ，我们顺势而为地定义“0！=1”就显得非常必要了。这样，组合数公式在 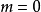及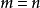 时也通行无阻，不会有任何尴尬了。

使用的广泛性

（1）在函数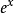 的麦克劳林级数展开式中 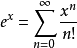明确地用到了“0！=1”的定义，没有这个定义就只能麻烦地表示为 。

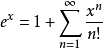（2）作为阶乘延拓的伽玛函数是定义在复数范围内的亚纯函数，与之有密切联系的函数还有贝塔函数（他们分别被称为欧拉第二积分与欧拉第一积分）。

拿伽玛函数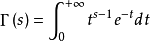 来说，显然有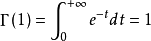

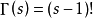当 是大于1的正整数时，有公式 ，当0的阶乘被定义为0！=1后，公式 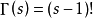对任意正整数 就都成立了。

为什么0！=1？

必须再次清楚地说明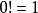： 只是一种定义出来的特殊的“形式”上的阶乘记号。它无法用演绎方法来论证。

“为什么0！=1”这个问题是伪问题，而初学者总要追问这个伪问题。这就说明了我们在教材和教学实践中都没有把**“有关‘0！=1’只是一种‘定义’的概念”**讲清楚。

有教辅材料上把上述必要性及合理性视作为推导的过程，那当然是大错特错了。必要性及合理性只是有限几个例子，“0！=1”这种定义是不能用举若干例子的方法来证明的。

但是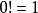 这个定义使用至今可谓久经考验方便多多，没有出现过任何逻辑上不合理的现象。

定义范围通常我们所说的阶乘是定义在自然数范围里的（大多科学计算器只能计算 0～69 的阶乘），小数科学计算器没有阶乘功能，如 0.5！，0.65！，0.777！都是错误的。但是，有时候我们会将Gamma 函数定义为非整数的阶乘，因为当 x 是正整数 n 的时候，Gamma 函数的值是 n－1 的阶乘。

伽玛函数（Gamma Function）定义伽马函数：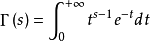

运用积分的知识，我们可以证明Γ（s）=（s）× Γ（s－1）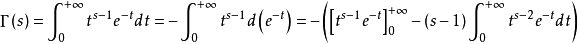

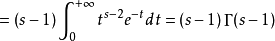
所以，当 x 是整数 n 时，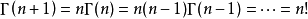

这样 Gamma 函数实际上就是阶乘的延拓。

计算机科学用Ruby求 365 的阶乘。

def AskFactorial(num) factorial=1;

step(num,1){|i| factorial*=i}

return factorial end factorial=AskFactorial(365)

puts factorial

阶乘有关公式该公式常用来计算与阶乘有关的各种极限。

此为斯特林公式的简化公式（完整的见下图）。

双阶乘双阶乘用“m！！”表示。

当 m 是自然数时，表示不超过 m 且与 m 有相同奇偶性的所有正整数的乘积。如：

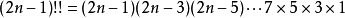
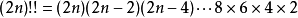
当 m 是负奇数时，表示绝对值小于它的绝对值的所有负奇数的绝对值积的倒数。

当 m 是负偶数时，m！！不存在。

自然数双阶乘比的极限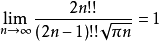

阶乘的逼近函数公式对于正整数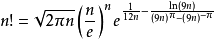

此逼近函数把近1 数处理到最小，函数指数误差详右侧图片

对于带小数大于1的正实数的阶乘计算公式为

（1）

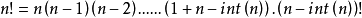
对于0.5到1之间的小数拟合公式如下：

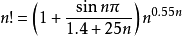
对于0到0.5之间的小数阶乘，先计算（1-n）!,再按一下公式计算：

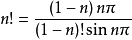计算时不要把先后顺序弄反，否则误差会增加，以上公式通过了伽马函数的校验，误差极小。

以下是拟合公式与实际值的对比图

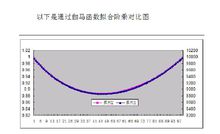
此处按（1）式拓展到负数区间，(-n)!的阶乘如下，但与词条定义冲突

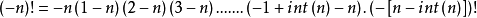
如此进一步计算为：

（2）
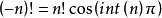这样把阶乘拓展到负数区间，形成了负数区间的周期震荡阶乘函数。

对于负小数-1