[科普中国]-玻耳兹曼统计

人物简介

路德维希·玻尔兹曼（Ludwig Edward Boltzmann，1844年2月20日-1906年9月5日），奥地利物理学家和哲学家，是热力学和统计物理学的奠基人之一。作为一名物理学家，他最伟大的功绩是发展了通过原子的性质（例如，原子量，电荷量，结构等等）来解释和预测物质的物理性质（例如，粘性，热传导，扩散等等）的统计力学，并且从统计意义对热力学第二定律进行了阐释。

玻尔兹曼的贡献主要在热力学和统计物理方面。1869年，他将麦克斯韦速度分布律推广到保守力场作用下的情况，得到了玻尔兹曼分布律。1872年，玻尔兹曼建立了玻尔兹曼方程（又称输运方程），用来描述气体从非平衡态到平衡态过渡的过程。1877年他又提出了著名的玻尔兹曼熵公式。2

原理表述全同粒子的经典统计法。又称麦克斯韦－玻耳兹曼统计或经典统计。考虑由同一种分子组成的气体。把每个分子看成近独立的子系统,它可能有Ki个能量为εi的状态。设有Ni个分子处于这组状态中。经典统计中对于状态的占有方式没有限制，而且每个分子都是可以识别的。把Ni个分子放到Ki个状态中的方式共有种，于是气体的熵满足：

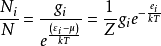其中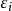：是第i个能量等级；μ是化学势；k是波尔兹曼常数；T是绝对温度；N是颗粒的总数；Z是分部函数。

在保证气体中总分子数和总能量一定的前提下，要求熵达到最大值,即可求得状态i的平均占有率或分布函数ni=Ni/Ki。为此应引入拉氏未定乘子α和ß，求解结果是(计算中使用斯特令近似公式lnNi=NlnN-N)

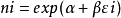
可以证明α=µ/T,ß=-1/T,µ是化学势，T是开尔文温度，这就是玻耳兹曼分布。它还可以从吉布斯正则分布，或作为量子统计法的极限得到。

应用麦克斯韦－玻耳兹曼统计可用于推导出麦克斯韦－玻耳兹曼分布（对于三维盒中的经典粒子的理想气体）。 但是，它们也适用于其他情况。 Maxwell-Boltzmann统计可用于将该分布扩展到具有不同能量 - 动量关系的粒子，如相对论粒子（Maxwell-Jüttner分布）。 此外，可以考虑假设情况，例如具有不同数量维数（四维，二维等）的盒子中的粒子。3

适用范围麦克斯韦 - 波尔兹曼统计量通常被描述为“可区分”的经典粒子的统计。换句话说，状态1中的粒子A和状态2中的粒子B的构造与粒子B处于状态1并且粒子A处于状态2的情况不同。该假设导致适当的（玻尔兹曼）统计能量状态的粒子，但是产生熵的非物理结果，如Gibbs悖论所体现的。

同时，没有真正的粒子具有麦克斯韦 - 波尔兹曼统计所要求的特性。事实上，如果我们把某种类型的所有粒子（例如电子，质子等）视为不可区分的话，吉布斯的悖论就被解决了，这个假设可以在量子力学的背景下证明。一旦做出这个假设，粒子统计数据就会改变。量子粒子是玻色子（代替Bose-Einstein统计）或费米子（遵循Pauli排除原则，而不是费米狄拉克统计）。这两个量子统计量在高温和低粒子密度的极限中接近麦克斯韦 - 波尔兹曼统计，而不需要任何特殊的假设。4

玻耳兹曼统计与吉卜斯系综统计玻耳兹曼统计法与吉卜斯系综统计法是统计物理中两种重要方法。这两种方法有不少相似之处也存在不少差异。

不同之处对系统的要求：对系统的要求玻耳获曼统计法（以下简称玻氏方法）只适用于由近独立粒子组成的孤立系统。而吉卜斯系综统计法（以下简称系综方法）适用于粒子间可以有相互作用的孤立系统、封闭系统或开放系统。

.描述系统微观状态的方法：为简单起见，设系统由N个全同粒子组成,且每个粒子的自由度数为r。在玻氏方法中,系统的微观状态由拼空间(它是由粒子的r个广义坐标和r个广义动量组成的2r维笛卡尔空间)，中N个代表点描述。由于玻氏方法所处理的是能量上彼此独立的拉子组成的系统，对于这种系统，由于在拼空间中当代表粒子状态的相点确定时，粒子的能量也就确定了，而与其他相点的位置无关，所以各相点具有统计独立性，因而用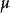空间来描写这种系统的状态是方便而合适的。

在系综方法中，由于组成系统的粒子之间可以有相互作用，所以当一个粒子的坐标与动量确定时，共能量是不确定的，它与其他粒子的相互作用势能及共他粒子的坐标有关，因此每个粒子不具有玻耳兹曼统计意义上的统计独立性，不能应用户空间来描述这类系统的状态。为解决这个困难，必须将整个系统作为一个整体来看待，这就需耍用系统的f=Nr个广义坐标q1,q2,…,qf及相应的f个广义动量p1,p2,...,pf构成系统的r空间来描写系统的状态。

可以从正则分布导出玻耳兹曼分布，反之，也可以从玻耳兹曼分布导出正则分布。’

相似之处两者都基于等几率假设，即假定处于统计平衡的孤立系统所有微观状态出现的几率相等。

玻耳兹曼分布与正则分布的函数形式相似，由它们导出的热力学公式的形式也相似。

当讨论由近独立粒子所组成的孤立系统时，两种统计法所得结果相同，两者是等价的。前面已提及最可儿分布井不穷尽全部可能的微观状态，但对于由很大数量的粒子组成的系统来说，由于热力学几率分布曲线在极大值附近非常陡，以致共他分布所对应的微观态数与最可几分布对应的微观态数相比非常少，可以忽略它们对宏观量的贡献。5

玻耳兹曼统计的应用同位素分离同位素分离在工业和科研上具有重要意义，被分离后的同位素在核反应、生物化学、地质化学研究方面有许多应用.如在和热中子反应中具有较大俘获截面、用来制作高致密度的吸收剂和屏蔽以及更高效的中子探测器。由于同位素的物理和化学性质的差异取决于质量的不同，因此可用离心机进行分离。将同位素气体分子放人半径为R的离心机转筒中，转筒以恒定角速度。筒内分子就处在恒定的惯性离心力场中，取和筒一起转动的坐标系。可见，不同质量的分子在相同的；处其密度不同，这样就可把它们分离开。

寻找激活介质激活介质是指在一定的外界条件下，它的某两个能级实现了粒子数反转并对特定频率的光基有放大作用的介质.制造激光器一定要有激活介质。因为不是任何物质的任意两个能级间都能实现粒子数反转的,因此必须寻找建立某两个能级间粒子数反转的条件。根据热平衡态下粒子数分布满足玻耳兹曼分布律而建立起的速率方程，可用来判断满足粒子数反转的条件。在原子体系中每个能级的粒子数变化可分成与外界辐射场有关的部分(受激项)和与外界作用无关的部分(弛豫项)。用体表示光对介质的激励概率，用P表示弛豫概率，它等于自发辐射概率与无辐射概率之和。

静电探针法测等离子体参数等离子体是电离气体，是物质的第四态。等离子体应用在受控热核反应、磁流体发电机和通讯、空间技术等各领域.等离子体中发生的一系列物理现象都与等离子体的性质和状态有关，因此测量等离子体的温度、电流一电压关系等参数是很重要的。静电探针是一种方便的测量方法，把探针插人等离子体中时，在等离子体和探针表面交界处会形成一个负电势的薄层，称为等离子体的“鞘”。这是因为热平衡时电子和离子的平均平动动能相等，而电子质量则小得多，所以电子的平均热运动速率比离子大，使一开始到达探针表面的电子数多于离子数,它们产生负电势阻止电子流的进一步增大，达平衡时，离子流和电子流密度相等，探针上电流为零，在探针表面就形成一层负电势的等离子体“鞘”。这时电子要从等离子体到达探针表面就必须克服由“鞘”形成的势垒，因此探针电势低于等离子体空间的电势。利用外电路逐渐改变探针的电势，可测得探针上的伏安特性曲线。当等离子体处于平衡时,电子能量服从麦克斯韦分布，则依靠热运动能量克服探针表面附近的负电势而到达探针表面的电子电流服从玻耳兹曼分布。6