[科普中国]-数列

由来三角形数

传说古希腊毕达哥拉斯（约公元前570-约公元前500年）学派的数学家经常在沙滩上研究数学问题，他们在沙滩上画点或用小石子来表示数。比如，他们研究过：

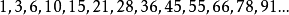
由于这些数可以用如右图所示的三角形点阵表示，他们就将其称为三角形数。

正方形数类似地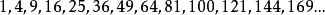， 被称为正方形数，因为这些数能够表示成正方形。因此，按照一定顺序排列的一列数称为数列。

概念函数解释数列的函数理解：

①数列是一种特殊的函数。其特殊性主要表现在其定义域和值域上。数列可以看作一个定义域为正整数集N*或其有限子集{1，2，3，…，n}的函数，其中的{1，2，3，…，n}不能省略。

②用函数的观点认识数列是重要的思想方法，一般情况下函数有三种表示方法，数列也不例外，通常也有三种表示方法：a.列表法；b。图像法；c.解析法。其中解析法包括以通项公式给出数列和以递推公式给出数列。

③函数不一定有解析式，同样数列也并非都有通项公式。

一般形式数列的一般形式可以写成

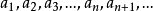
简记为{an}。

项数列中的项必须是数，它可以是实数，也可以是复数。

用符号{an}表示数列，只不过是“借用”集合的符号，它们之间有本质上的区别：**1.**集合中的元素是互异的，而数列中的项可以是相同的。**2.**集合中的元素是无序的，而数列中的项必须按一定顺序排列，也就是必须是有序的。

分类（1）有穷数列和无穷数列：

项数有限的数列为“有穷数列”（finite sequence）；

项数无限的数列为“无穷数列”（infinite sequence）。

（2）对于正项数列：（数列的各项都是正数的为正项数列）

1）从第2项起，每一项都大于它的前一项的数列叫做递增数列；如：1，2，3，4，5，6，7；

2）从第2项起，每一项都小于它的前一项的数列叫做递减数列；如：8，7，6，5，4，3，2，1；

3）从第2项起，有些项大于它的前一项，有些项小于它的前一项的数列叫做摆动数列（摇摆数列）；

（3）周期数列：各项呈周期性变化的数列叫做周期数列（如三角函数）；

（4）常熟数列：各项相等的数列叫做常数数列（如：2，2，2，2，2，2，2，2，2**）**。

公式（1）通项公式：数列的第N项an与项的序数n之间的关系可以用一个公式an=f(n)来表示，这个公式就叫做这个数列的通项公式，如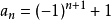 。数列通项公式的特点：1）有些数列的通项公式可以有不同形式，即不唯一；2）有些数列没有通项公式（如：素数由小到大排成一列2，3，5，7，11，...）。

（2）递推公式：如果数列{an}的第n项与它前一项或几项的关系可以用一个式子来表示，那么这个公式叫做这个数列的递推公式。数列递推公式特点：1）有些数列的递推公式可以有不同形式，即不唯一。2）有些数列没有递推公式，即有递推公式不一定有通项公式。

等差数列定义一般地，如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，这个数列就叫做等差数列（arithmetic sequence），这个常数叫做等差数列的公差（common difference），公差通常用字母d表示，前n项和用Sn表示。等差数列可以缩写为A.P.（Arithmetic Progression）1。

通项公式an=a1+(n-1)d

其中，n=1时 a1=S1；n≥2时 an=Sn-Sn-1。

an=kn+b(k,b为常数) 推导过程：an=dn+a1-d 令d=k，a1-d=b 则得到an=kn+b。

等差中项由三个数a，A，b组成的等差数列堪称最简单的等差数列。这时，A叫做a与b的等差中项（arithmetic mean）。有关系：A=(a+b)÷2。

前n项和倒序相加法推导前n项和公式：

Sn=a1+a2+a3 +·····+an=a1+(a1+d)+(a1+2d)+······+[a1+(n-1)d] ①

Sn=an+an-1+an-2+······+a1=an+(an-d)+(an-2d)+······+[an-(n-1)d] ②

由①+②得2Sn=(a1+an)+(a1+an)+······+(a1+an)（n个）=n(a1+an)

∴Sn=n(a1+an)÷2。

等差数列的前n项和等于首末两项的和与项数乘积的一半：

Sn=n(a1+an)÷2=na1+n(n-1)d÷2

Sn=dn2÷2+n(a1-d÷2)

亦可得

a1=2sn÷n-an

an=2sn÷n-a1

有趣的是S2n-1=(2n-1)an，S2n+1=(2n+1)an+1

性质（1）任意两项am，an的关系为：an=am+(n-m)d，它可以看作等差数列广义的通项公式。

（2）从等差数列的定义、通项公式，前n项和公式还可推出：a1+an=a2+an-1=a3+an-2=…=ak+an-k+1，k∈N*。

（3）若m，n，p，q∈N*，且m+n=p+q，则有am+an=ap+aq。

（4）对任意的k∈N*，有Sk，S2k-Sk，S3k-S2k，…，Snk-S(n-1)k…成等差数列。

应用日常生活中，人们常常用到等差数列如：在给各种产品的尺寸划分级别时，当其中的最大尺寸与最小尺寸相差不大时，常按等差数列进行分级。若为等差数列，且有an=m，am=n，则am+n=0。其于数学的中的应用，可举例：快速算出从23到132之间6的整倍数有多少个，算法不止一种，这里介绍用数列算令等差数列首项a1=24（24为6的4倍），等差d=6；于是令an= 24+6(n-1)