定义
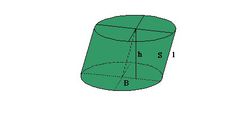
1、如右图,以矩形的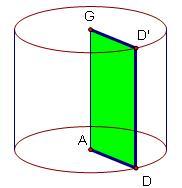 一边所在直线为旋转轴,其余三边旋转360°形成的曲面所围成的几何体叫作圆柱(circular cylinder),即矩形ADD'G的一条边AG为轴,其余三边旋转一周所得的几何体。其中AG叫做圆柱的轴,AG叫做圆柱的高,无论旋转到什么位置不垂直于轴的边都叫做圆柱的母线
一边所在直线为旋转轴,其余三边旋转360°形成的曲面所围成的几何体叫作圆柱(circular cylinder),即矩形ADD'G的一条边AG为轴,其余三边旋转一周所得的几何体。其中AG叫做圆柱的轴,AG叫做圆柱的高,无论旋转到什么位置不垂直于轴的边都叫做圆柱的母线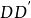 。DA和D'G旋转形成的两个圆叫做圆柱的底面,DD'旋转形成的曲面叫做圆柱的侧面。
。DA和D'G旋转形成的两个圆叫做圆柱的底面,DD'旋转形成的曲面叫做圆柱的侧面。
2、在同一个平面内有一条定直线和一条动线,当这个平面绕着这条定直线旋转一周时,这条动线所成的面叫做旋转面,这条定直线叫做旋转面的轴,这条动线叫做旋转面的母线。如果母线是和轴平行的一条直线,那么所生成的旋转面叫做圆柱面。如果用垂直于轴的两个平面去截圆柱面,那么两个截面和圆柱面所围成的几何体叫做直圆柱,简称圆柱。
分类直圆柱直圆柱也叫正圆柱、圆柱,就是底面和顶面是同样半径(r)的圆,并且两圆圆心的连线和顶面、底面的互相垂直,并且我们可以得知,圆柱侧面展开图是长方形1。
高:h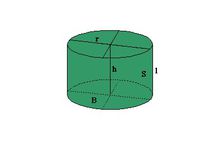
底面半径:r
底面直径:d
侧面积:S
总表面积:T
体积:V
底面积:A;B
S=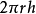
T=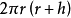
V=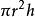
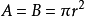
d=2r
斜圆柱所谓的圆柱就是顶面和底面是同样半径(r)的圆,两圆圆心的连线和顶面、底面不互相垂直,并且我们可以得知,圆柱侧面展开图是平行四边形。
S=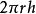
T=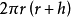
V=Ah=Bh=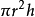
圆柱的底面是两个完全相等的圆,圆锥只有一个底面是个圆。
两个底面之间的距离叫做圆柱的高。圆柱有无数条高,且高的长度都相等。圆锥的顶点到底面圆心的距离叫做圆锥的高,圆锥只有一条高。
圆柱和圆锥的侧面是曲面。但圆柱的侧面展开图是正方形或长方形(沿高剪),而圆锥的侧面展开图是一个扇形。
体积圆柱所占空间的大小,叫做这个圆柱体的体积.
求圆柱的体积跟求长方体、正方体一样,都是底面积×高。
设一个圆柱底面半径为r,高为h,则圆柱的体积为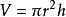
S为底面积,高为h,体积为V,三者关系为: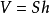 ,其中,
,其中,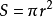
面积计算圆柱的侧面积=底面的周长×高。2
S侧=Ch(C表示底面的周长,h表示圆柱的高)
圆柱的底面积=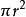
圆柱的表面积
圆柱的表面积=侧面积+两个底面积(S表=S侧+2S底)
S表=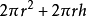
S侧=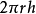
S底=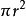
组成名称圆柱的两个完全相同的圆面叫做底面(又分上底和下底);圆柱有一个曲面,叫做侧面;两个底面的对应点之间的距离叫做高(高有无数条)。
特征:
1、圆柱的底面都是圆,并且大小一样。
2、圆柱两个面之间的垂直距离叫做高,把圆柱的侧面打开,得到一个矩形,这个矩形的一条边就是圆柱的底面周长。
与圆锥的关系等底等高的圆锥积是圆柱体积的三分之一。
体积和高相等的圆锥与圆柱,圆锥的底面积是圆柱的三倍。
体积和底面积相等的圆锥与圆柱,圆锥的高是圆柱的三倍。
等底等高间圆柱与圆锥之间的侧面积之比关系为: S圆柱侧/S圆锥侧=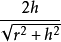
 ,其中,r为底面半径,h为高。
,其中,r为底面半径,h为高。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国