[科普中国]-双曲线

简介

在数学中，双曲线（多重双曲线或双曲线）是位于平面中的一种平滑曲线，由其几何特性或其解决方案组合的方程定义。双曲线有两片，称为连接的组件或分支，它们是彼此的镜像，类似于两个无限弓。双曲线是由平面和双锥相交形成的三种圆锥截面之一。 （其他圆锥部分是抛物线和椭圆，圆是椭圆的特殊情况）如果平面与双锥的两半相交，但不通过锥体的顶点，则圆锥曲线是双曲线。

双曲线出现在许多方面：

作为在笛卡尔平面中表示函数{\ displaystyle f（x）= 1 / x} f（x）= 1 / x的曲线，

作为日后的阴影的路径，

作为开放轨道（与闭合的椭圆轨道不同）的形状，例如在行星的重力辅助摆动期间航天器的轨道，或更一般地，超过最近行星的逃逸速度的任何航天器，

作为一个单一的彗星（一个旅行太快无法回到太阳系）的路径，

作为亚原子粒子的散射轨迹（以排斥而不是吸引力作用，但原理是相同的），

在无线电导航中，当距离到两点之间的距离而不是距离本身可以确定时，

等等。

双曲线的每个分支具有从双曲线的中心进一步延伸的更直（较低曲率）的两个臂。对角线对面的手臂，一个从每个分支，倾向于一个共同的线，称为这两个臂的渐近线。所以有两个渐近线，其交点位于双曲线的对称中心，这可以被认为是每个分支反射以形成另一个分支的镜像点。在曲线{\ displaystyle f（x）= 1 / x} f（x）= 1 / x的情况下，渐近线是两个坐标轴。

双曲线共享许多椭圆的分析属性，如偏心度，焦点和方向图。许多其他数学物体的起源于双曲线，例如双曲抛物面（鞍形表面），双曲面（“垃圾桶”），双曲线几何（Lobachevsky的着名的非欧几里德几何），双曲线函数（sinh，cosh，tanh等）和陀螺仪矢量空间（提出用于相对论和量子力学的几何，不是欧几里得）。1

名称定义我们把平面内与两个定点F1,F2的距离的差的绝对值等于一个常数(常数为2a，小于|F1F2|)的轨迹称为双曲线;平面内到两定点的距离差的绝对值为定长的点的轨迹叫做双曲线2）

即：│|PF1|-|PF2│|=2a

定义1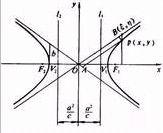：平面内，到两个定点的距离之差的绝对值为常数（小于这两个定点间的距离2）的点的轨迹称为双曲线。定点叫双曲线的焦点。

定义2：平面内，到给定一点及一直线的距离之比为常数e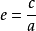（ （e>1），即为双曲线的离心率）的点的轨迹称为双曲线。定点叫双曲线的焦点，定直线叫双曲线的准线。双曲线准线的方程为 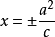（焦点在x轴上）或 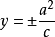（焦点在y轴上）。

定义3：一平面截一圆锥面，当截面与圆锥面的母线不平行也不通过圆锥面顶点，且与圆锥面的两个圆锥都相交时，交线称为双曲线。

定义4：在平面直角坐标系中，二元二次方程F(x,y)=ax2+bxy+cy2+dx+ey+f=0满足以下条件时，其图像为双曲线2。

1.a、b、c不都是零.

2.Δ=b2 - 4ac > 0.

注：第2条可以推出第1条。

在高中的解析几何中，学到的是双曲线的中心在原点，图像关于x，y轴对称的情形。这时双曲线的方程退化为： .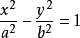

上述的四个定义是等价的，并且根据建好的前后位置判断图像关于x，y轴对称。

标准方程为：

1、焦点在X轴上时为：

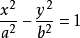(a>0,b>0)

2、焦点在Y 轴上时为：

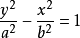(a>0,b>0)

特征介绍以下从纯几何的角度给出一些双曲线的相关概念和性质。

分支可以从图像中看出，双曲线有两个分支。当焦点在x轴上时，为左轴与右轴；当焦点在y轴上时，为上轴与下轴。

焦点在定义1中提到的两个定点称为该双曲线的焦点，定义2中提到的一给定点也是双曲线的焦点。双曲线有两个焦点。焦点的横（纵）坐标满足c²=a²+b²。

准线在定义2中提到的给定直线称为该双曲线的准线。

离心率在定义2中提到的到给定点与给定直线的距离之比，称为该双曲线的离心率。

离心率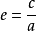

双曲线有两个焦点，两条准线。(注意:尽管定义2中只提到了一个焦点和一条准线,但是给定同侧的一个焦点,一条准线以及离心率可以根据定义2同时得到双曲线的两支,而两侧的焦点,准线和相同离心率得到的双曲线是相同的。)

顶点双曲线和它的对称轴有两个交点,它们叫做双曲线的顶点。

实轴两顶点之间的距离称为双曲线的实轴,实轴长的一半称为实半轴。

虚轴在标准方程中令x=0,得y²=-b²，该方程无实根，为便于作图，在y轴上画出B1(0,b)和B2(0,-b),以B1B2为虚轴.

渐近线双曲线有两条渐近线。渐近线和双曲线不相交。

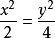渐近线的方程求法是：将右边的常数设为0，即可用解二元二次的方法求出渐近线的解，例如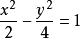： ,将1替换为0,得,则双曲线的渐近线为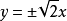

一般地我们把直线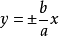 叫做双曲线(焦点在X轴上)的渐近线(asymptote to the hyperbola )

焦点在y轴上的双曲线的渐近线为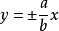

顶点连线斜率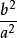 双曲线 y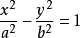 上一点与两顶点连线的斜率之积为。

实际应用双曲线在实际中的应用有通风塔，冷却塔，埃菲尔铁塔，广州塔等。

面积公式若 ∠F1PF2=θ，

则 S△F1PF2=b2×cot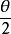 或S△F1PF2=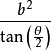

·例：已知F1、F2为双曲线C：x2－y2=1的左右焦点，点P在C上，∠F1PF2=60°，则P到x轴的距离为多

少？

解：由双曲线焦点三角形面积公式得:

S△F1PF2=b2×cot( )=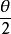

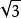
设P到x轴的距离为h，则 S△F1PF2 =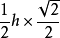 ; h =参数方程

重点取值范围2│x│≥a(焦点在x轴上)或者│y│≥a(焦点在y轴上)。

对称性关于坐标轴和原点对称，其中关于原点成中心对称。

顶点A(-a,0) ， A'(a,0）。同时 AA'叫做双曲线的实轴且│AA'│=2a。

B(0,-b） ， B'(0,b）。同时 BB'叫做双曲线的虚轴且│BB'│=2b。

F1（-c,0)或（0，-c） , F2（c,0）或（0，c）。F1为双曲线的左焦点，F2为双曲线的右焦点且│F1F2│=2c

对实轴、虚轴、焦点有：a2+b2=c2

渐近线焦点在x轴:。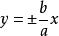

焦点在y轴: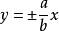. 圆锥曲线ρ=ε/1-ecosθ当e>1时，表示双曲线。其中p为焦点到准线距离，θ为弦与x轴夹角。

令1-ecosθ=0可以求出θ，这个就是渐近线的倾角，即θ=arccos（1/e)

令θ=0，得出ρ=ε/（1-e）,x=ρcosθ=ε/（1-e）

令θ=π，得出ρ=ε/（1+e）,x=ρcosθ=-ε/（1+e）

这两个x是双曲线定点的横坐标。

求出它们的中点的横坐标（双曲线中心横坐标）

x=[(ε/1-e)+(-ε/1+e)]/2

（注意化简一下）

直线ρcosθ=[(ε/1-e)+(-ε/1+e)]/2

是双曲线一条对称轴，注意是不与曲线相交的对称轴。

将这条直线顺时针旋转π/2-arccos（1/e）角度后就得到渐近线方程，设旋转后的角度是θ’

则θ’=θ-[π/2-arccos（1/e)]

则θ=θ’+[π/2-arccos（1/e)]

代入上式：

ρcos{θ’+[π/2-arccos（1/e)]}=[(ε/1-e)+(-ε/1+e)]/2

即：ρsin[arccos（1/e)-θ’]=[(ε/1-e)+(-ε/1+e)]/2

然后可以用θ取代式中的θ’了

得到方程：ρsin[arccos（1/e)-θ]=[(ε/1-e)+(-ε/1+e)]/2

现证明双曲线x2/a2-y2/b2=1 上的点在渐近线中

设M(x,y）是双曲线在第一象限的点，则

y=(b/a）√（x2-a2） (x>a)

因为x2-a20)

Y2/(-2c) - X2/(-2c) = 1 (c1；

在双曲线的线上称为双曲线上，则有x2/a2-y2/b2=1；在双曲线所夹的区域称为双曲线外，则有x2/a2-y2/b2