高斯消去法,又称高斯消元法,实际上就是我们俗称的加减消元法。数学上,高斯消去法或称高斯-约当消去法,由高斯和约当得名(很多人将高斯消去作为完整的高斯-约当消去的前半部分),它是线性代数中的一个算法,用于决定线性方程组的解,决定矩阵的秩,以及决定可逆方矩阵的逆。当用于一个矩阵时,高斯消去产生“行消去梯形形式”。高斯消去法,又称高斯消元法,实际上就是我们俗称的加减消元法。 数学上,高斯消去法或称高斯-约当消去法,由高斯和约当得名(很多人将高斯消去作为完整的高斯-约当消去的前半部分),它是线性代数中的一个算法,用于决定线性方程组的解,决定矩阵的秩,以及决定可逆方矩阵的逆。当用于一个矩阵时,高斯消去产生“行消去梯形形式”。例如:一个二元一次方程组,设法对每个等式进行变形,使两个等式中的同一个未知数的系数相等,这两个等式相减,得到一个新的等式,在这个新的等式中,细数相等的未知数就被除去了(系数为0)。同样的也适合多元多次方程组。
简述高斯消去法,又称高斯消元法,实际上就是我们俗称的加减消元法。数学上,高斯消去法或称高斯-约当消去法,由高斯和约当得名(很多人将高斯消去作为完整的高斯-约当消去的前半部分),它是线性代数中的一个算法,用于决定线性方程组的解,决定矩阵的秩,以及决定可逆方矩阵的逆。当用于一个矩阵时,高斯消去产生“行消去梯形形式”。高斯消去法,又称高斯消元法,实际上就是我们俗称的加减消元法。
数学上,高斯消去法或称高斯-约当消去法,由高斯和约当得名(很多人将高斯消去作为完整的高斯-约当消去的前半部分),它是线性代数中的一个算法,用于决定线性方程组的解,决定矩阵的秩,以及决定可逆方矩阵的逆。当用于一个矩阵时,高斯消去产生“行消去梯形形式”。例如:一个二元一次方程组,设法对每个等式进行变形,使两个等式中的同一个未知数的系数相等,这两个等式相减,得到一个新的等式,在这个新的等式中,细数相等的未知数就被除去了(系数为0)。同样的也适合多元多次方程组。
高丝消去法 - 信息学方面的应用
历史该方法以数学家卡尔·高斯命名,但最早出现于中国古籍《九章算术》,成书于约公元前150年。
例子高斯消元法可用来找出下列方程组的解或其解的限制:
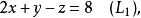
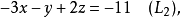
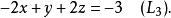
这个算法的原理是:
首先,要将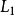 以下的等式中的
以下的等式中的 消除,然后再将
消除,然后再将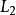 以下的等式中的
以下的等式中的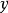 消除。这样可使整个方程组变成一个三角形似的格式。之后再将已得出的答案一个个地代入已被简化的等式中的未知数中,就可求出其余的答案了。
消除。这样可使整个方程组变成一个三角形似的格式。之后再将已得出的答案一个个地代入已被简化的等式中的未知数中,就可求出其余的答案了。
在刚才的例子中,我们将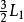 和
和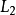 相加,就可以将
相加,就可以将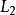 中的
中的 消除了。然后再将
消除了。然后再将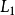 和
和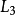 相加,就可以将
相加,就可以将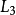 中的
中的 消除。
消除。
我们可以这样写:
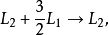
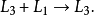
结果就是:
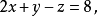
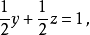
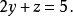
现在将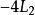 和
和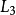 相加,就可将
相加,就可将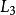 中的
中的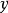 消除:
消除:
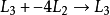
其结果是:
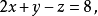
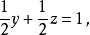
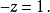
这样就完成了整个算法的初步,一个三角形的格式(指:变数的格式而言,上例中的变数各为3,2,1个)出现了。
第二步,就是由尾至头地将已知的答案代入其他等式中的未知数。第一个答案就是:
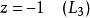
然后就可以将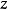 代入
代入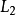 中,立即就可得出第二个答案:
中,立即就可得出第二个答案:
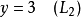
之后,将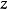 和
和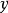 代入
代入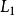 之中,最后一个答案就出来了:
之中,最后一个答案就出来了:
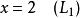
就是这样,这个方程组就被高斯消元法解决了。
这种算法可以用来解决所有线性方程组。即使一个方程组不能被化为一个三角形的格式,高斯消元法仍可找出它的解。例如,如果在第一步化简后,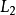 及
及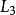 中没有出现任何
中没有出现任何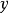 ,没有三角形的格式,照着高斯消元法而产生的格式仍是一个行梯阵式。这情况之下,这个方程组会有超过一个解,当中会有至少一个变数作为答案。每当变数被锁定,就会出现一个解。
,没有三角形的格式,照着高斯消元法而产生的格式仍是一个行梯阵式。这情况之下,这个方程组会有超过一个解,当中会有至少一个变数作为答案。每当变数被锁定,就会出现一个解。
通常人或电脑在应用高斯消元法的时候,不会直接写出方程组的等式来消去未知数,反而会使用矩阵来计算。以下就是使用矩阵来计算的例子:
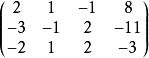
跟着以上的方法来运算,这个矩阵可以转变为以下的样子:
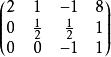
这矩阵叫做“行梯阵式”。
最后,可以利用同样的算法产生以下的矩阵,便可把所得出的解或其限制简明地表示出来:
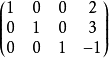
最后这矩阵叫做“简化行梯阵式”,亦是高斯-约当消元法指定的步骤。
其他应用找出逆矩阵高斯消元法可以用来找出一个可逆矩阵的逆矩阵。设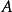 为一个
为一个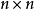 的矩阵,其逆矩阵可被两个分块矩阵表示出来。将一个
的矩阵,其逆矩阵可被两个分块矩阵表示出来。将一个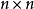 单位矩阵放在
单位矩阵放在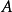 的右手边,形成一个
的右手边,形成一个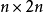 的分块矩阵
的分块矩阵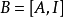 。经过高斯消元法的计算程序后,矩阵
。经过高斯消元法的计算程序后,矩阵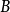 的左手边会变成一个单位矩阵
的左手边会变成一个单位矩阵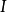 ,而逆矩阵
,而逆矩阵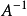 会出现在
会出现在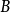 的右手边。
的右手边。
假如高斯消元法不能将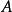 化为三角形的格式,那就代表
化为三角形的格式,那就代表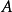 是一个不可逆的矩阵。
是一个不可逆的矩阵。
应用上,高斯消元法极少被用来求出逆矩阵。高斯消元法通常只为线性方程组求解。
计出秩的基本算法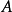 高斯消元法可应用在任何
高斯消元法可应用在任何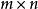 的矩阵。在不可减去某数的情况下,我们都只有跳到下一行。以一个
的矩阵。在不可减去某数的情况下,我们都只有跳到下一行。以一个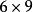 的矩阵作例,它可以变化为一个行梯阵式:
的矩阵作例,它可以变化为一个行梯阵式:

而矩阵中的*'是一些数字。这个梯阵式的矩阵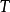 会有一些关于
会有一些关于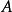 的资讯:
的资讯:
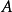 的秩是5,因为
的秩是5,因为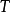 有5列非0的列;
有5列非0的列;
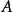 的行的向量空间Col(A),可从
的行的向量空间Col(A),可从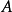 的第1、3、4、7和9行中得知,其数值在矩阵{\displaystyle T}之中;
的第1、3、4、7和9行中得知,其数值在矩阵{\displaystyle T}之中;
矩阵中的*'表示了的列可怎样写为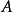 列中的数的组合1。
列中的数的组合1。
分析高斯消元法的算法复杂度是O(n);这就是说,如果系数矩阵的是n×n,那么高斯消元法所需要的计算量大约与n成比例。
高斯消元法可以用在电脑中来解决数千条等式及未知数。不过,如果有过百万条等式时,这个算法会十分费时。一些极大的方程组通常会用迭代法来解决。亦有一些方法特地用来解决一些有特别排列的系数的方程组。
高斯消元法可用在任何域中。
高斯消元法对于一些矩阵来说是稳定的。对于普遍的矩阵来说,高斯消元法在应用上通常也是稳定的,不过亦有例外2。
伪代码高斯消元法的其中一种伪代码:
i = 1 j = 1 while (i ≤ m and j ≤ n) do Find pivot in column j, starting in row i // 从第i列(row)开始,找出第j行(column )中的最大值(i、j值应保持不变) #台湾与中国的列、行定义相反。台湾列为row行为column,中国列为column行为row。 maxi = i for k = i+1 to m do if abs(A[k,j]) > abs(A[maxi,j]) then maxi = k // 使用交换法找出最大值(绝对值最大) end if end for if A[maxi,j] ≠ 0 then // 判定找到的绝对值最大值是否为零:若不为零就进行以下操作;若为零则说明该列第(i+1)列以下(包括第(i+1)列)均为零,不需要再处理,直接跳转至第(j+1)行第(i+1)列 swap rows i and maxi, but do not change the value of i // 将第i行与找到的最大值所在行做交换,保持i值不变(i值记录了本次操作的起始行) Now A[i,j] will contain the old value of A[maxi,j]. divide each entry in row i by A[i,j] // 将交换后的第i列归一化(第i列所有元素分别除以A[i,j]) Now A[i,j] will have the value 1. for u = i+1 to m do // 第j行中,第(i+1)列以下(包括第(i+1)列)所有元素都减去A[i,j],直到第j行的i+1列以後元素均为零 subtract A[u,j] * row i from row u Now A[u,j] will be 0, since A[u,j] - A[i,j] * A[u,j] = A[u,j] - 1 * A[u,j] = 0. end for i = i + 1 end if j = j + 1 // 第j行中,第(i+1)列以下(包括第(i+1)列)所有元素均为零。移至第(j+1)行,从第(i+1)列开始重复上述步骤。 end while这个算法和之前谈到的有点不同,它由绝对值最大的部分开始做起,这样可以改善算法的稳定性。本算法由左至右地计算,每作出以下三个步骤,才跳到下一行和下一列:
定出每行的绝对值最大的一个非0的数,将第一列的值与该列交换,使得第一列拥有这一行的最大值;
将第一行的数字除以该数,使得该列的第一个数成为1;
对每一列减去第一列乘以每一列的第一个数,使得每一列的第一个数变为0。
所有步骤完成后,这个矩阵会变成一个列梯矩阵,再用代入法就可以求解该方程组。
随着多核处理器的日益普及,现在的程序员可以利用线程级并行高斯消元算法来提高计算的速度。内存共享模式(而不是消息交换模式)的伪代码如下所示3:
// Note this code sample has been mangled (missing attr init/scope? bad gauss() indentation?)...// What is original source? Can we get valid C or else simplified pseudo code instead of this hybrid? void parallel(int num_threads,int matrix_dimension) { int i; for(i=0;icur_count=0; pthread_cond_broadcast(&(mybarrier->barrier_cond)); } pthread_mutex_unlock(&(mybarrier->barrier_mutex)); }本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国