[科普中国]-granger因果检验

简介

经济学家开拓了一种可以用来分析变量之间的因果的办法，即格兰杰因果关系检验。该检验方法为2003年诺贝尔经济学奖得主克莱夫·格兰杰（Clive W. J. Granger）所开创，用于分析经济变量之间的因果关系。他给因果关系的定义为“依赖于使用过去某些时点上所有信息的最佳最小二乘预测的方差。”

在时间序列情形下，两个经济变量X、Y之间的格兰杰因果关系定义为：若在包含了变量X、Y的过去信息的条件下，对变量Y的预测效果要优于只单独由Y的过去信息对Y进行的预测效果，即变量X有助于解释变量Y的将来变化，则认为变量X是引致变量Y的格兰杰原因。

进行格兰杰因果关系检验的一个前提条件是时间序列必须具有平稳性，否则可能会出现虚假回归问题。因此在进行格兰杰因果关系检验之前首先应对各指标时间序列的平稳性进行单位根检验（unit root test)。常用增广的迪基—富勒检验(ADF检验)来分别对各指标序列的平稳性进行单位根检验。

当X时间序列的由于“格兰杰原因”导致了Y序列，X序列在一段时间的迟滞后，引起了Y序列的大致重复（可见图中箭头所指示），则X序列可以作为未来序列Y的预测。1

格兰杰在2003年诺贝尔获奖时曾提出，“很多人把格兰杰因果关系用在了非经济学领域，从而得出了很多‘荒唐’的结论”，“当然，很多‘荒唐’的论文也随之出现”。1

核心概念过去值过去值（lag value，或称落後期）：同一变项比当期时间上更早的值。例如：当期为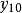 ，它的落後期为 。

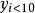格兰杰因果关系检验的基本观念在于：未来的事件不会对目前与过去产生因果影响，而过去的事件才可能对现在及未来产生影响。也就是说，如果我们试图探讨变数x是否对变数y有因果影响，那么只需要估计x的落後期是否会影响y的现在值，因为x的未来值不可能影响y的现在值。假如在控制了y变数的过去值以后，x变数的过去值仍能对Y 变数有显著的解释能力，我们就可以称x能“Granger 影响”（Granger-cause）y。2

局限性和改进最初版的格兰杰因果测试，有时候无法发现真正的因果关系。因为虽然对于认定因果关系而言，理论上还必须控制其他可能的干扰因素，但在 Granger 最初提出这套因果测试的版本中，并未纳入干扰变数的分析，而是假设其他可能解释变数的资讯包含在y的落后值中。如果事实上带来因果关系的是第三变数（干扰变数），亦即若事实上操控x并无法改变y，格兰杰因果关系的零假设仍然可能被拒绝。因此标准版的格兰杰因果测试结果可能会产生误导性。

1980年代由其他的计量经济学家对Granger测试加以修改、扩充，将可能的第三（以上）变数纳入测试，成为使用面板资料的向量自回归模型（英语：panel data VAR model）。相较于最初版的 Granger 测试，扩充版可以产生更有效的估计结果。2

步骤描述准备工作：一开始要用几个落後期来建立模型，需要研究者的评估，通常使用赤池信息量准则（英语：Akaike information criterion、简称AIC） 或贝斯信息量准则（英语：Bayesian information criterion、简称BIC）来判断。

格兰杰因果关系检验的第一步是建立用y的落後期来预测y的自回归模型。此际，如果时间序列y是广义平稳的，则可以直接使用落後期。如果不平稳，就必须对不平稳的时间序列先做（一阶或更多阶）差分，直到得出平稳时间数列。

如果发现y的某期落後期 (1) 在回归分析中具有显著性（根据t检定的p值来判断），且 (2) 这期落後期加入模型后可提高回归模型的解释力（根据回归分析的F检定），这个落後期便被留在模型中。

然后进一步加入x（或Δx）的滞后期来扩充回归模型。关于平稳时间序列的要求、某期落後期留在模型中的条件，同上述y的处理。

当且仅当（充分必要）没有任何解释变项x（或Δx）的落後期被留在模型中，便无法拒绝无格兰杰因果关系的零假设。

研究人员希望发现明显的证据，比如x是y的格兰杰原因但反之不成立，便能做出因果关系的推论。然而在实际操作中也可能会发现没有变量是对方的格兰杰原因，或者x和y两个变量互为格兰杰原因。3

数学定义1. 令x和y为广义平稳序列。如要检测x非y的格兰杰原因之零假设，首先引入y的落後期建立y的自回归模型（AR model ony）：

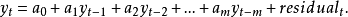
所有的y落後期中：(1) 在回归分析中具有显著性（根据t-统计值的p值来判断）的，且 (2) 这期落後期加入模型后可提高回归模型的解释力（根据回归分析的F检定）的－－将被留在模型中。m表示的是y变量滞后期中检定为显著的时间上最早一个。

2. 接着，引入x的落後期建立增广回归模型：

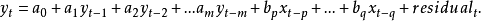
所有的{\displaystyle x}落後期中：(1) 在回归分析中具有显著性（根据学生t检验的p值来判断）的，且 (2) 这期落後期加入模型后可提高回归模型的解释力（根据回归分析的F检定）的－－将被留在模型中。在以上增广回归模型中，p代表x变量落後期中检定为显著的时间上最早一个，q则是x变量落後期中检定为显著的时间上最近一个。

3. 如果没有任何x的落後期被留在模型中，无格兰杰因果关系的零假设就成立。3

延伸承继著回归模型的基本性质，格兰杰因果关系分析也假设实际值与预测值之间的误差呈正态分布，若实际现象不呈正态分布将严重影响推论的有效性。

Hacker & Hatemi-J (2006)发展出一种不必在乎误差项是否呈正态分布的格兰杰因果关系研究方法。这种方法在财金分析上特别实用， 因为许多金融变量不服从正态分布。

近来，Hacker & Hatemi-J (2012)又进一步改善之，提出一种非对称的因果关系检验模型，据说可以区分正向与负向影响的因果影响。3