超限数的研究是根据数学理论发展的需要提出来的,自从1883年德国数学家康托尔(1829 一1920) 建立集合 论以来,集合论的思想和方法已经渗透到各个领域。在数学研究对象中,更多的是无穷集合,用什 么 样 的 数刻 划无穷集合元素个数的无穷程度成了研究无穷集合的一个重要问题。十九世纪末期 ,康托尔首先进行了超限数的 研究,基本上解决了这一 问题,使超限数的思想和方法成了今日数学的基础1。
超限数是大于所有有限数(但不必为绝对无限)的基数或序数。分别叫做超穷基数和超穷序数。
术语“超限”(transfinite)是康托尔提出的,他希望避免词语无限(infinite)和那些只不过不是有限(finite)的那些对象有关的某些暗含。当时其他的作者少有这些疑惑;现在被接受的用法是称超限基数或序数为无限的。但是术语“超限”仍在使用。
超穷序数可以确定超穷基数,并导出阿列夫数序列。
对于有限数,有两种方式考虑超限数,作为基数和作为序数。不像有限基数和序数,超限基数和超限序数定义了不同类别的数。
含义1.最小超限序数是ω。
2.第一个超限基数是aleph-0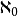 ,整数的无限集合的势。如果选择公理成立,下一个更高的基数是aleph-1
,整数的无限集合的势。如果选择公理成立,下一个更高的基数是aleph-1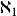 。如果不成立,则有很多不可比较于aleph-1并大于aleph-0的其他基数。但是在任何情况下,没有基数大于aleph-0并小于aleph-1。
。如果不成立,则有很多不可比较于aleph-1并大于aleph-0的其他基数。但是在任何情况下,没有基数大于aleph-0并小于aleph-1。
连续统假设声称在aleph-0和连续统(实数的集合)的势之间没有中间基数:就是说,aleph-1是实数集合的势。已经在数学上证实了连续统假设不能被证明为真或假,由于不完备性的影响。
某些作者,比如Suppes、Rubin使用术语超限基数来称呼戴德金无限集合的势,在可以不等于无限基数的上下文中;就是说在不假定可数选择公理成立的上下文中。给定这个定义,下列是等价的2:
1)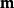 是超限基数。就是说有一个戴德金无限集合
是超限基数。就是说有一个戴德金无限集合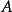 使得
使得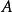 的势是
的势是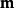 ;
;
2)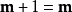 ;
;
3)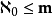 ;
;
4)有一个基数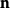 使得
使得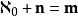 。
。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国