[科普中国]-相对离散指标

基本介绍定义

包括全距、平均差和标准差等标志变动度都是绝对指标，都有与平均指标相同的计量单位。各种标志变动度的数值大小，不仅受离散程度的影响，而且还受数列水平(即标志本身的水平)高低的影响。因此，在对比分析中，不宜直接使用上述各种标志变异指标来比较不同水平数列之间的标志离散程度，必须用反映标志变异程度的相对指标来比较，即用离散系数比较。

相对离散指标也叫离散系数、变异系数或标准差系数，是变量的标准差与均值之比，通常用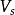来表示，即:

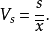离散系数越大，说明变量分布的离散程度越强，平均数的代表性越差；离散系数越小，说明变量分布的离散程度越弱，平均数的代表性越好。

标准差标准差又称均方差，是指各变量值与算术平均数相减之差的平方的算术平均数的平方根。它是测定变量变动度最常用的重要指标。标准差充分利用了所有统计资料，而且便于代数运算。标准差考虑了总体各变量变动的影响，比平均差更符合实际，所以在抽样推断上具有很重要的作用。标准差的计算公式为:

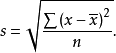式中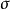：——标准差；

——各个变量值；

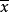——算术平均值；

——总变量数。

例题解析例1 以下是两个不同水平的工人日产量(件) 资料：

甲组：60，65，70，75，80

乙组：2，5，7，9，12

由此计算得：甲的平均数70件，甲的标准差为7.07件；乙的平均数为7件，乙的标准差为3.41件。

若根据标准差甲大于乙而断言，甲组离散程度大于乙组，或乙组的平均数代表性高于甲组，都是不妥的。因为这两组的水平悬殊，应计算其离散系数来比较：甲的离散系数根据公式算得10.1%，乙的离散系数根据公式算得48.7%，计算结果表明，并非甲组离散程度大于乙组，而是乙组大于甲组，或者说，乙组的平均日产量代表性低于甲组2。

**注意：**全距、四分位差，平均差和标准差等都是反映变量分布离散程度的绝对指标，其数值大小取决于变量值本身水平即均值水平的高低，并且都有明确的计量单位。因此，不同均值水平和不同计量单位的绝对离散指标是不能直接比较的。为了不同变量分布之间离散程度的可比性，必须消除不同均值水平和不同计量单位的影响，应该计算相对离散指标3。