[科普中国]-螺旋运动

螺旋运动(helicoidal motion)是一种空间变换，指空间中一个旋转和一个移动方向与旋转轴平行的平移变换之积。旋转的轴也称为螺旋运动的轴，旋转的角也称螺旋运动的角。螺旋运动是一种空间运动，其逆变换仍是螺旋运动。两螺旋运动的积是一个螺旋运动。任意一个螺旋运动可以分解为两个轴反射之积，这两个轴反射的反射轴是异面直线。空间的螺旋运动分两类，若用弯曲的右手指表示构成螺旋运动的“旋转”方向时，伸直的拇指恰表示构成螺旋运动的“移动”方向，则称该螺旋运动是右螺旋运动，否则称为左螺旋运动。平移是旋转角为零的螺旋运动，旋转是平移距离为零的螺旋运动。当螺旋运动不是平移或旋转时，没有不动点，而轴是惟一的不动线，又假如螺旋运动的角不等于kπ(k∈Z)，则它也没有不动面1。

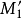基本概念定义一所谓螺旋运动，是指一个旋转R和一个平移T的合成运动，平移沿着旋转的轴。这两个过程的顺序无关重要(如果平移不是沿着旋转的轴，情况就不同了)，换言之，设M为一点(如下图)，沿轴D旋转一个给定的角度至(这旋转记作R)，再将平行于D作一确定的平移T到达新位置；如果先将M用平移T到达，再将绕轴D作旋转R，那么依然来到同样的位置。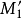

事实上，设m为两点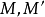在轴上的公共射影，而为之射影，则图形显然可由图形利用平移得出。那么前者就和后者一样是一个等腰三角形，它的平面垂直于D而顶角等于R的转幅，这就证明了断言的正确性。

螺旋运动显然包括旋转(当平移T为零时)和平移(当旋转R为零时)作为特殊情况。

**备注：**当我们已知一个螺旋运动时，在轴上就确定了一个正向，即平移的指向。因此，我们说一个螺旋运动是正的(或右手的)，或者反过来说是逆的(或左手的)，就看沿着平移的正向所作的旋转是正的还是逆的2。

定义二由绕轴 的旋转和沿着 方向与旋转角成比例的移动而合成的运动，称为螺旋运动(图1)。轴 称为螺旋轴。

若 是旋转角(螺旋角)而 是进给(平移距离)，则有： 。

比例因子 ，称为螺旋参数。若顺着移动方向观察一个螺旋，当旋转为顺时针方向时，这个螺旋为右螺旋，当旋转为逆时针方向时，这个螺旋为左螺旋。

可以用p的正负号来确定螺旋的方向：

：右螺旋，

：左螺旋。

定理1 螺旋运动由绕一条轴的旋转和沿轴向与旋转角成比例的移动而形成，它是由螺旋轴，螺旋参数和螺旋方向，(右螺旋或左螺旋)所确定的。

螺旋运动的基本作图已知 点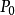 和垂直于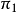 的螺旋轴 的水平投影和正面投影，螺旋参数p和螺旋角 。

求作 从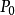 转过螺旋角 至P的这段螺旋轨迹的水平投影和正面投影。

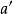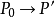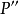在水平投影中，螺旋运动投影为绕 旋转 角的转动： 。 在过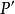 的连系线上。并比 高出进给 的距离。这段距离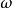 可以往参数圆(圆心为 ，半径为p)上取对应于圆心角 的弧而作出。最好用尽可能短的弦求出这段弧长。 ·

转过一个整圈 的平移距离 ，称为螺旋的导程。由它可以按照

计算出螺旋参数。p也称为转换导程。

螺旋体几何形体通过螺旋运动形成螺旋体。

点通过螺旋运动形成作为轨迹曲线的螺旋线(轨迹螺旋线)；

曲线通过螺旋运动形成为运动曲面的螺旋面；

曲面通过螺旋运动形成为包络面的螺旋面。

一切螺旋体都可自相旋合。由于这个缘故，它们在工程中得到应用。

螺旋线1. 以p为螺旋参数，当P点绕轴作螺旋运动时，其轨迹螺旋线b位于螺旋柱面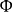 (以 为轴、半径 的回转柱面)上。

由于 ，所以在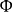 展开后，b成为一条直线。因此，螺旋线b与 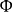的各条素线e相交成定角 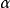，对此有

于是b的切线对的每个法面成定坡度。螺旋线b是同坡线(对的每个法面而言)。

2. 若将b的切线平移到上一点R处，则它们形成b的准锥面(顶点为R、轴线为和半张角为的回转锥面，图2)。螺旋运动的两个导圆中的“第一个导圆”，称为螺旋线b的准圆。准圆平面在R“之下”的距离为p。

任一螺旋切线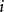，都垂直于通过其切点P的螺旋柱面半径。由此得出：

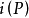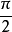螺旋切线平行于通过准点P*的准锥面素线，P*在准圆上，与交点相差角(图3)

定理2 每条螺旋线都是螺旋轴的各个法面的同坡线，也是常曲率空间曲线。它的密切平面和切线，都与螺旋轴构成相同的角3。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学